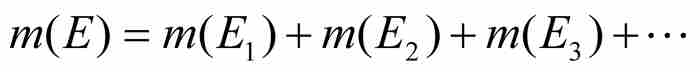微積分的歷程：從牛頓到勒貝格：第14章勒貝格_William Dunham

亨利·勒貝格（1875—1941）

隨著20世紀的到來，數學家們有理由為自己喝彩。微積分已經存在了兩個多世紀。它的基礎已經不容置疑，許多懸而未決的問題已經宣告解決。自從牛頓和萊布尼茨初創微積分以來，分析學走過了漫長的路程。

適逢其時，亨利·勒貝格捲入到這門學科中來。他在1902年對積分論進行了革命，並且進一步把這場革命推進到實分析，那時他還是巴黎大學的一名才華橫溢的博士生。他以一篇博士論文實現了這一目標，那篇論文被描述成「以往所有數學家寫就的最佳論文之一」。1

1 引自G. T. Q. Hoare and N. J. Lord, 「『Integrale, longueur, aire'—the centenary of the Lebesgue integral」, The Mathematical Gazette, vol. 86 (2002), p. 3。

為了對勒貝格的成就獲得一些感性認識，在考察勒貝格富有創造性的替代積分之前，我們快速複習一下黎曼積分。

回歸黎曼積分

在前面幾章已經著重指出黎曼積分中存在的某些「缺陷」。由於這個原因，數學家們曾經期待是正確的命題，需要附加某些假設方能成為真命題。例如，如果不給出看起來過份限制的假設，微積分基本定理以及極限與積分的交換定理都不復成立。

對於後一種情況，在第9章舉出的反例中包含一個函數序列，函數項帶有越來越高的尖峰值。在那種情況下，人們可能認為極限與積分不能交換的原因在於函數不是一致有界的。然而從下面的例子明顯看出，這種缺陷隱藏得更深。

我們從區間[0, 1]中的有理數集開始，這個集合用Q_{1表示。集合的可數性使我們能夠把它列舉出來：Q_{1={r_{1, r_{2, r_{3, r_{4, …}。然後我們定義函數序列}}}}}}

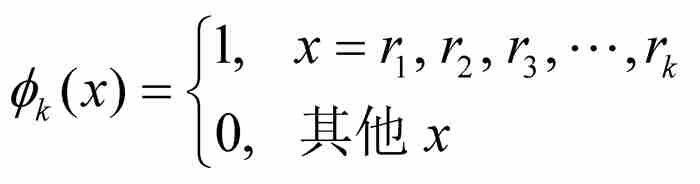
其中在前面k個有理數點都取值1，而在其餘的點取值0，每個這樣的函數是有界函數，滿足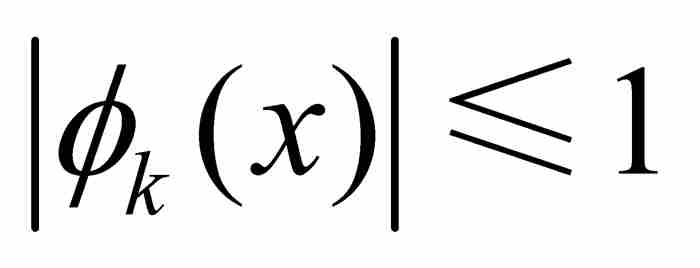，同時每個函數在除有限個點以外等於0，所以是可積的，並且。

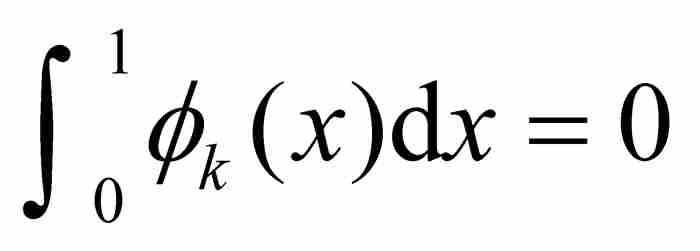但是，關於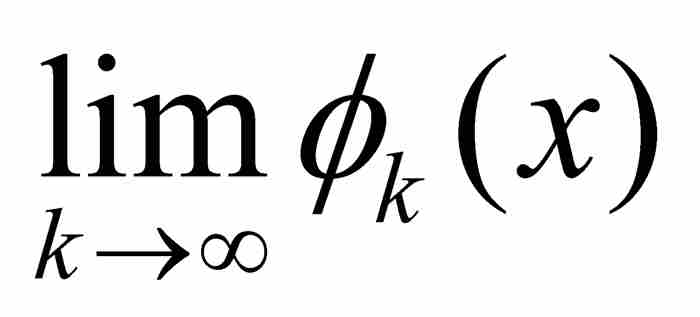會有什麼結果？由於[0, 1]中的任何有理數位於列表中的某處地方，當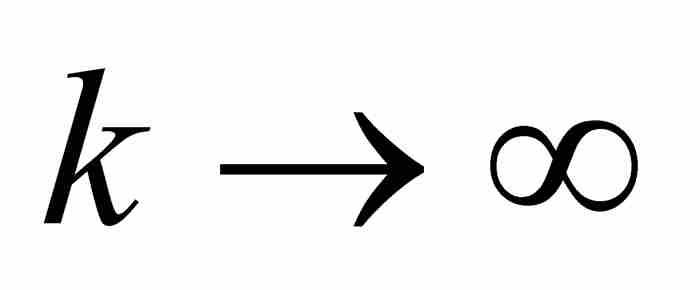時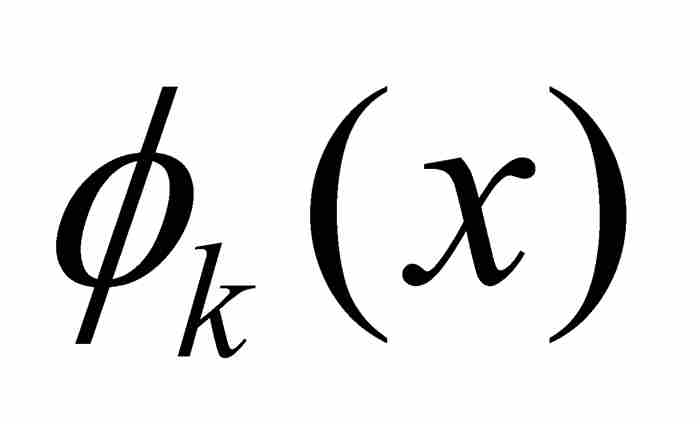最終將取值1，並且保持這個值。此外，如果x為無理數，對於所有k有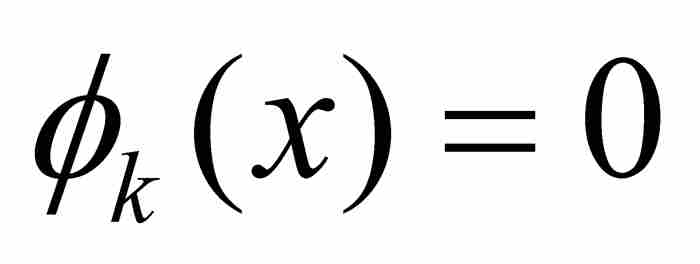。換句話說，

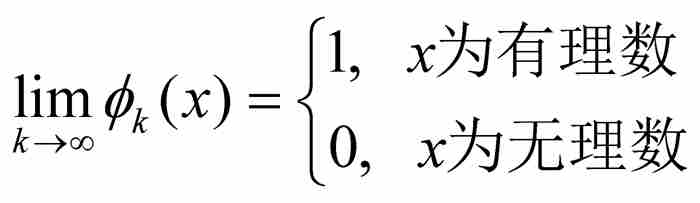（1）

自然，我們得到的是狄利克雷函數，所以縱然每個是可積的，它們的點態極限是不可積的。不言而喻，狄利克雷函數的不可積性表明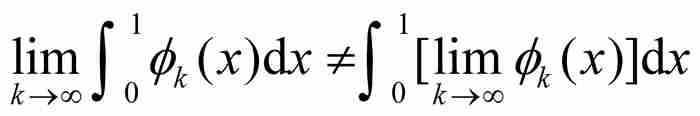，。這意味著，在第9章的例子中，積分與極限的交換問題不能用函數的無界性來解釋。

即使對這些問題作了考慮，仍然留下如何通過不連續性說明黎曼可積性的特徵的問題。按照前面一章所用的函數不連續性點集的記號，數學家們期待著填寫下列句子：

（2）

任何人都相信，這個句子中的空白將會用關於函數的不連續性點集D_f的某種「小型性」的條件填入。顯而易見，這個缺少的條件不會是「有限的」或「可數的」，也不會是「第1類集合」，它的特性是不確定的。無論是誰，如果憑借函數的連續性與黎曼可積性之間的聯繫，完成上述句子的填充，定然引起巨大轟動。

正是勒貝格解決了所有這些問題。他回歸到長度和面積的概念，從全新的角度觀察它們，並由此提出積分的一種替代定義。我們的故事就從我們現在所說的「勒貝格測度」開始。

零測度

在1904年的一本專著《積分與原函數的研究》中，勒貝格這樣描述他的最初目標：「我希望首先對集合賦予數的屬性，這種數類似於它們的長度。」 2 這本專著脫胎於它的學位論文。

1 Henri Lebesgue, Lecons sur l'integration et la recherche des fonctions primitives, Gauthier-Villars, 1904, p. 36。

他從非常簡單的情況開始。在四個區間[a, b]，(a, b]，[a, b)和(a, b)中，任何一個區間的長度均為b-a。如果一個集合是兩個不相交集合的並集，也就是說，如果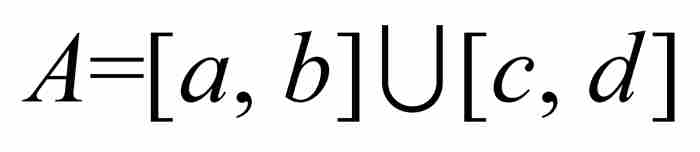，其中b<c，那麼我們自然令A的長度為（b-a）+（d-c）。按同樣的方式，我們可以給出任何有限個不相交區間的並集的長度。

但是，勒貝格已經注意到複雜得多的集合。例如，我們應該怎樣把長度的概念擴充到像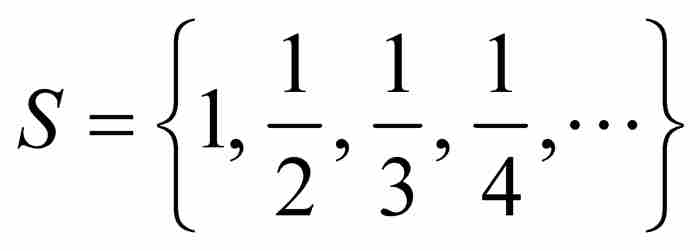這樣的無限集合上？在第13章曾經證明，集合S是無處稠密的。或者換一種說法，我們如何度量包含在單位區間[0, 1]內的無理數集合的「長度」？

在勒貝格之前的數學家中有人曾經提出過這些問題。阿克捨爾·哈納克（1851—1888）在19世紀80年代引進過集合的一種度量，我們現在稱之為有界集的外容量。3 當給定這樣的一個集合時，他先把它置於有限個區間的一個覆蓋內，並且用這些區間的長度的和作為集合外容量的近似值。對於上述集合S，我們可以考慮覆蓋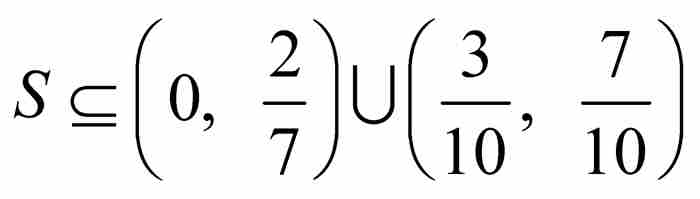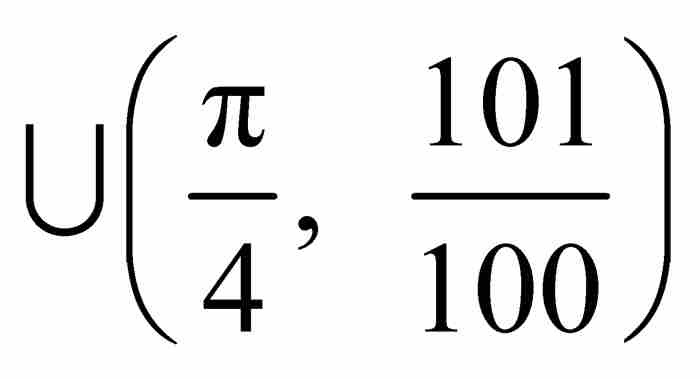，它們的長度之和等於。

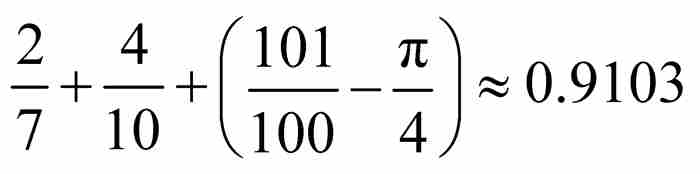2 Thomas Hawkins, Lebesgue's Theory of Integration, Chelsea, 1975, p. 63。

我們可以通過取一個不同的覆蓋來改進這個估值。例如，假定我們用下面5個子區間的並集覆蓋S：

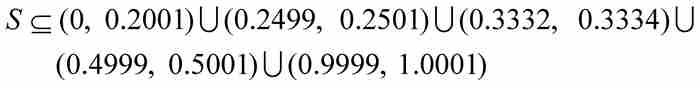
雖然這樣做顯得有些奇怪，不過我們的策略是清楚的（參見圖14-1）。最左邊的區間（0, 0.2001）包含S中除1/4, 1/3, 1/2和1以外的所有點，而這4個點都用各自的小區間包圍。對於這個覆蓋，其區間的長度之和為0.2001+0.0002+0.0002+ 0.0002+0.0002=0.2009，比前面第一個覆蓋的長度值0.9103小得多。

圖　14-1

至此，哈納克提出了一個大膽的想法：用有限個區間以所有可能的方式覆蓋一個有界集合E，再求每個覆蓋中各區間長度之和，並把外容量c_e(E)定義為當最寬區間的長度趨近零時這種和的極限。

這個定義有許多可取之處。例如，一個有界區間的外容量就是它的長度——這恰好是人們所期望的。同樣，單點集{a}的外容量必定為零，因為對於任何自然數k，我們可以用一個長度為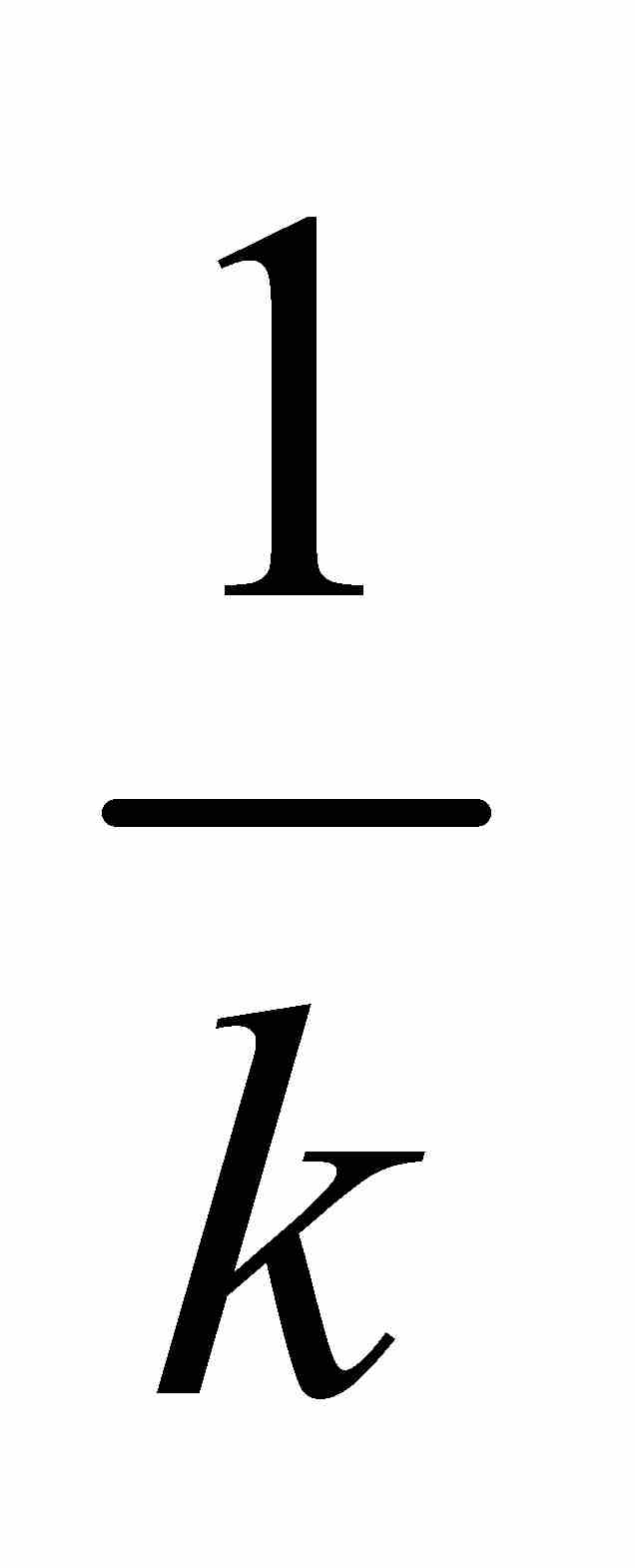的區間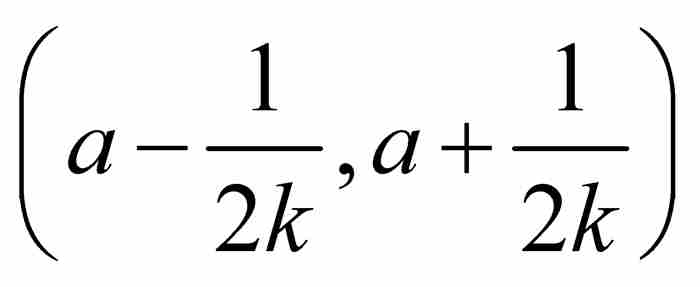覆蓋｛a｝，當k不斷增大時，這個長度縮小為零，所以c_e({a})=0。這也是如人們所期望的。

哈納克同樣能求出像S那樣的無限集的外容量。他用的是上面第二個覆蓋中所顯示的方法。對於任何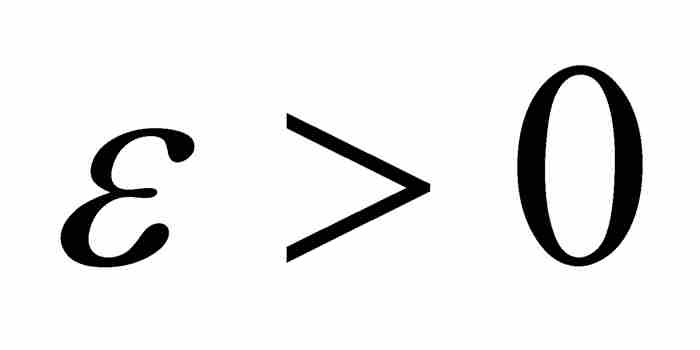，我們注意區間（0, 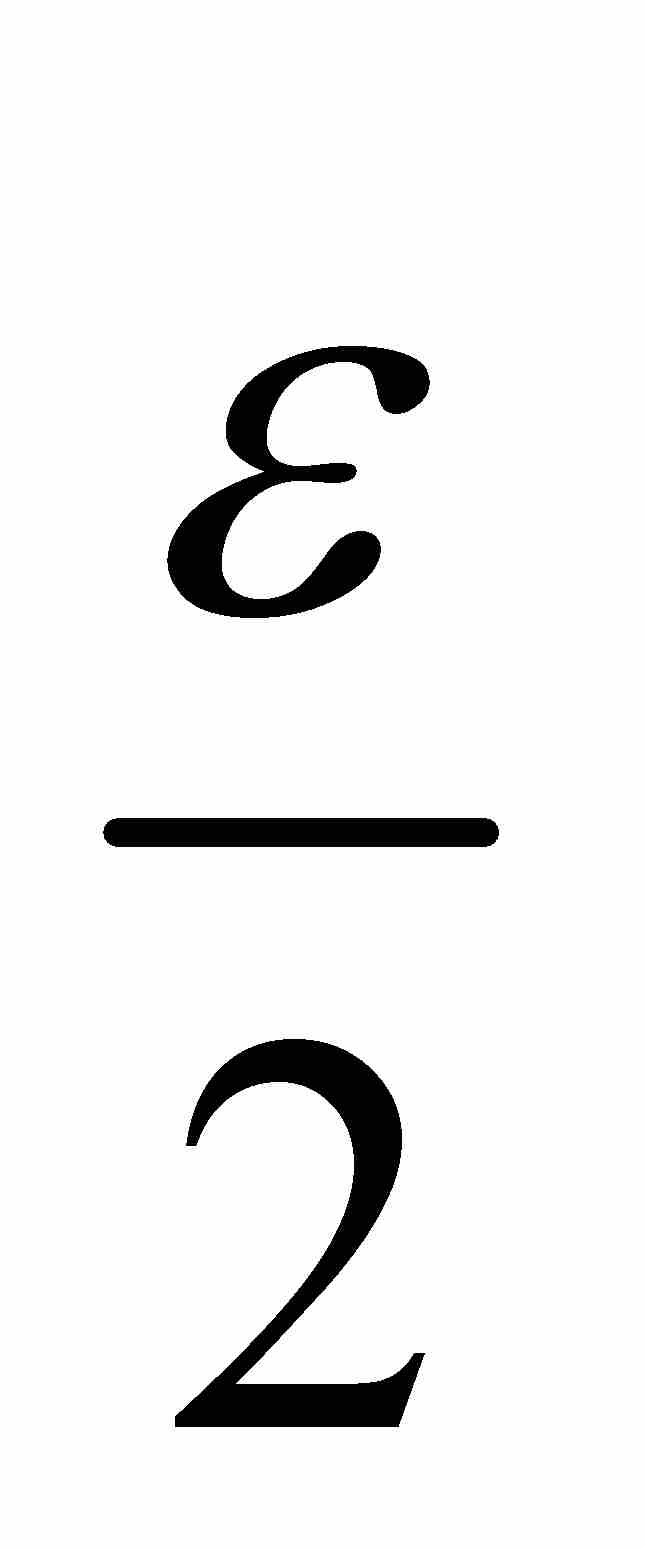）包含S中除有限個點以外的所有點，我們用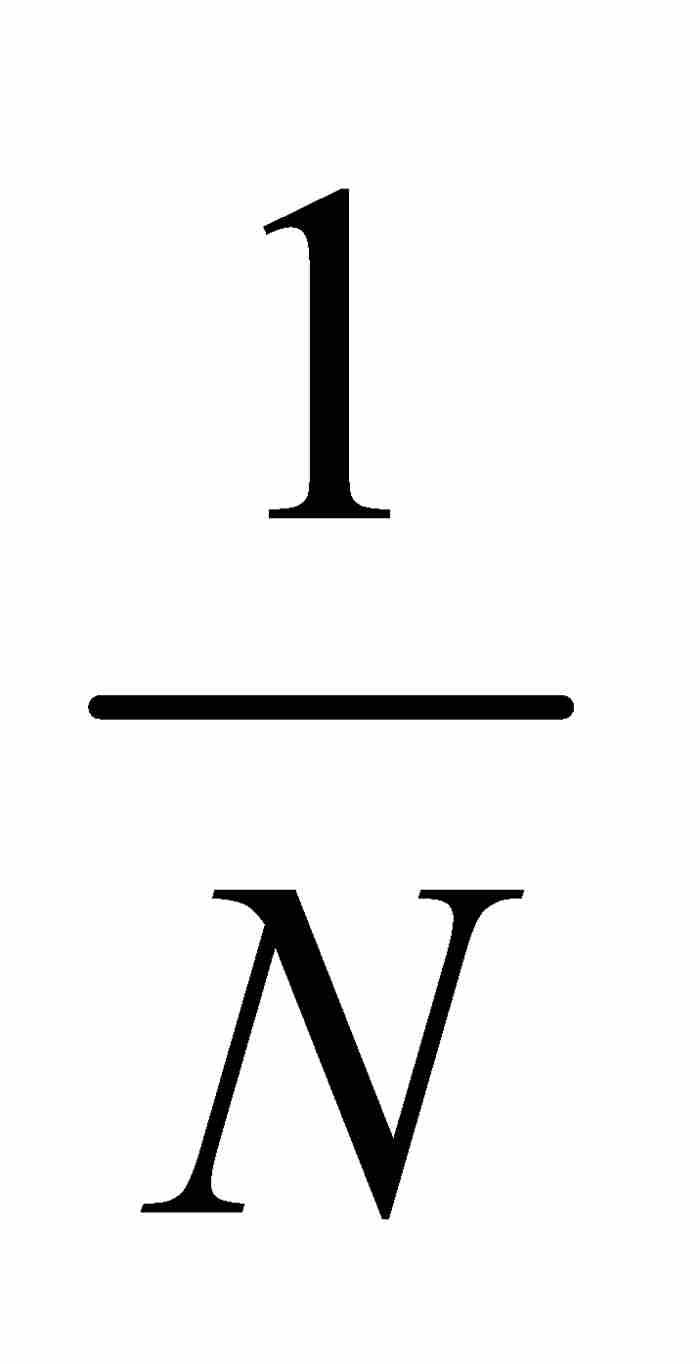, , 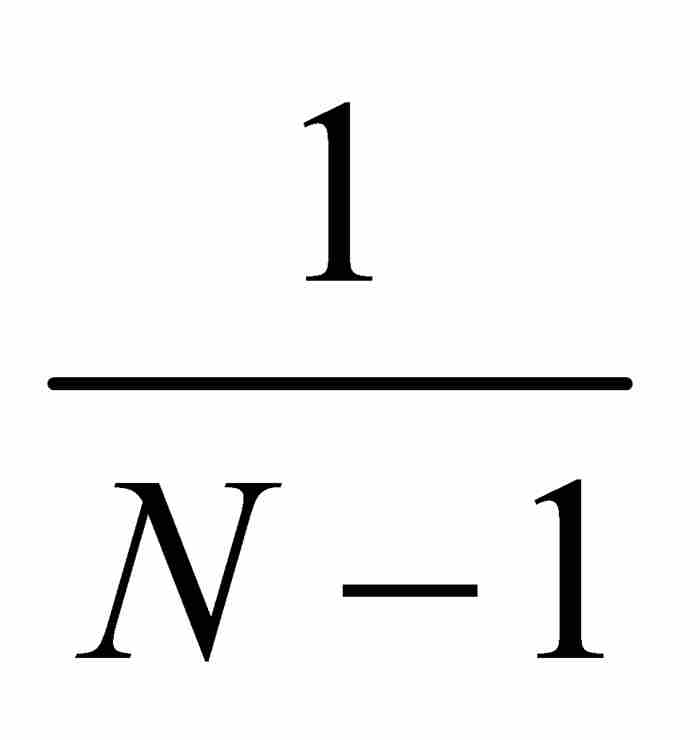…, 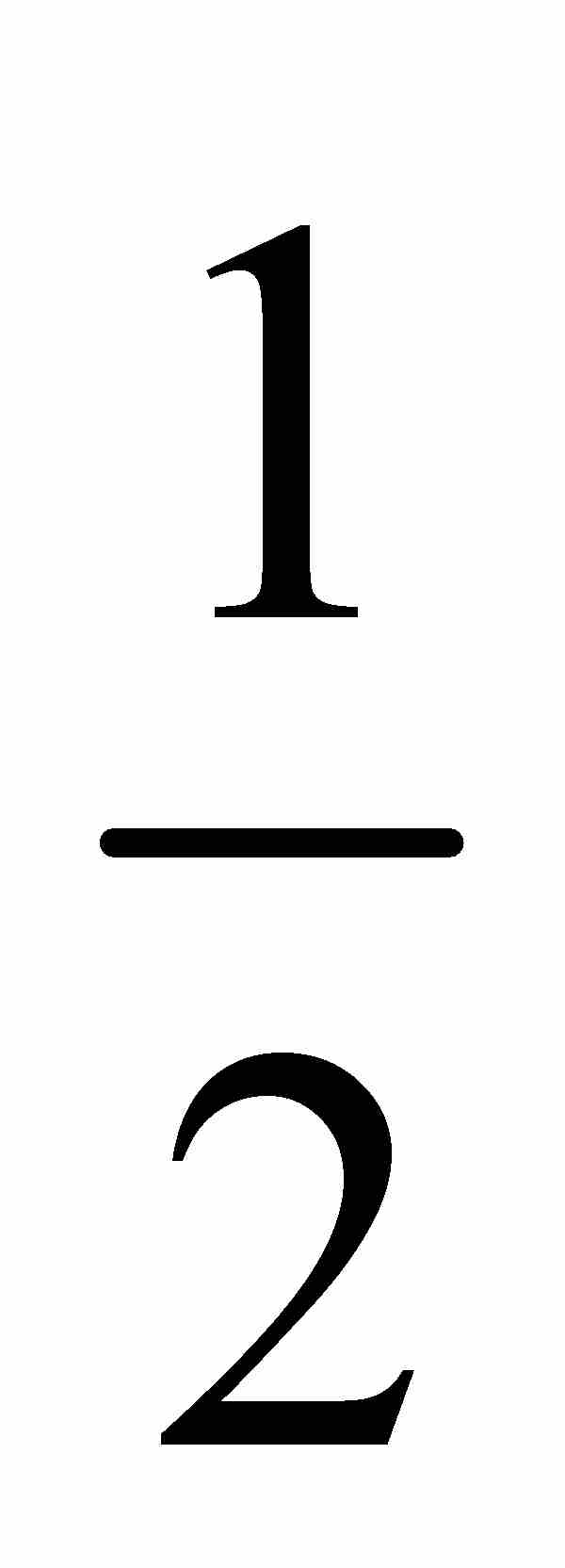和1表示這有限個點。然後把這N個點置於一個長度為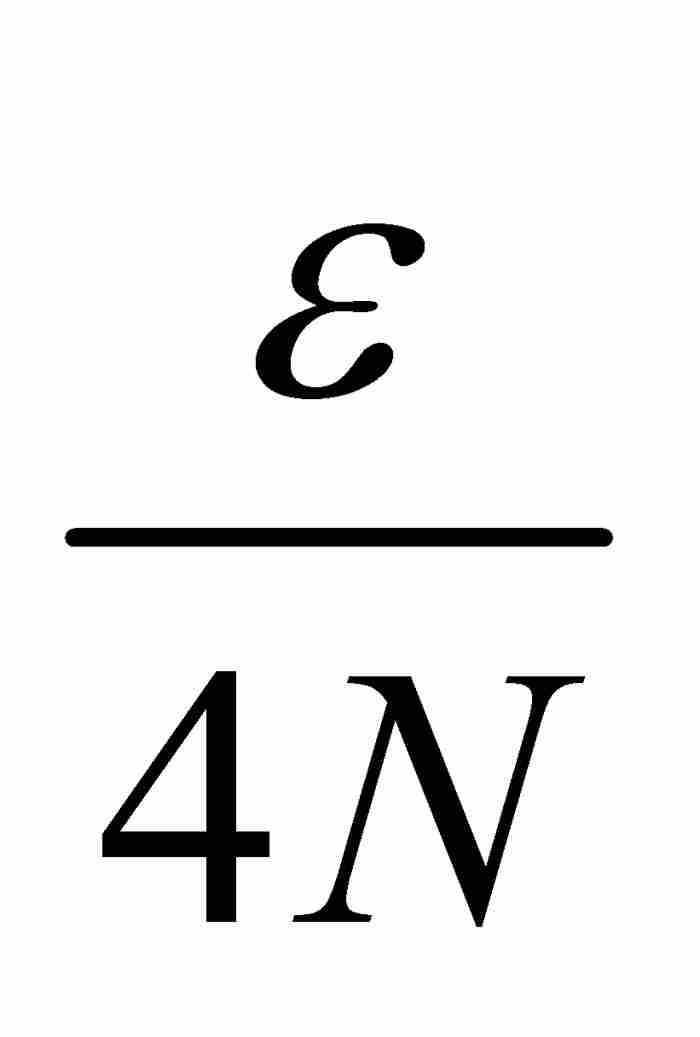的小區間內。例如，可以把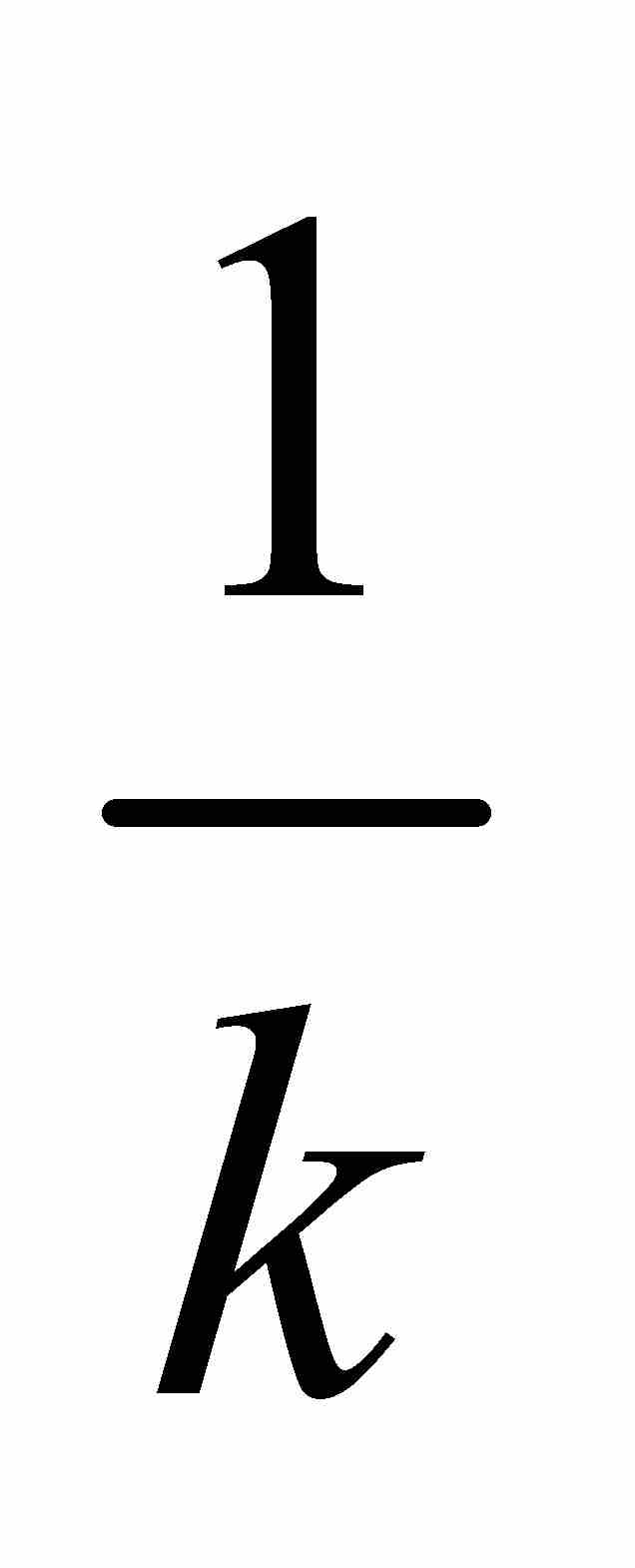置於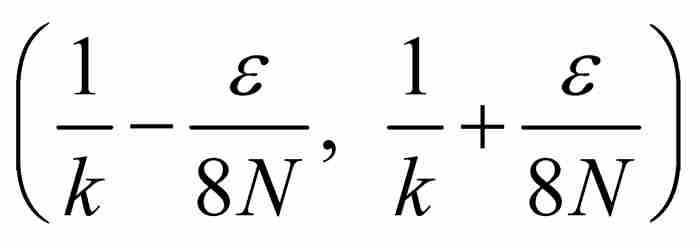內。這些區間共同覆蓋S，而它們的長度之和為

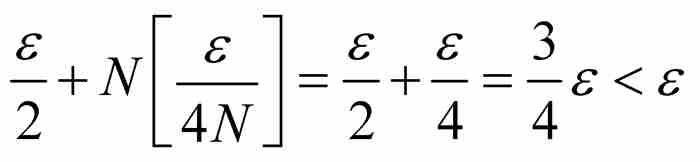
由於對每個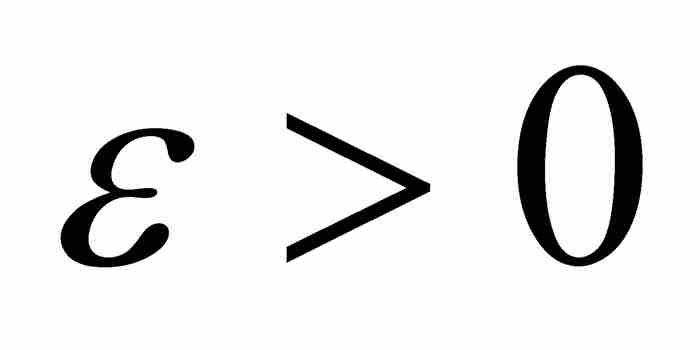，S處於總長度小於ε的有限個區間內，所以我們斷定c_e(S)=0。這樣就得到一個外容量為零的無限的無處稠密集。

但是，哈納克要面對一種不同的情況，那就是區間[0, 1]內的有理數的集合Q_{1：一個無限的稠密集。他認識到，由有限個區間構成的Q_{1的任何覆蓋必然覆蓋整個[0, 1]區間。因此c_e(Q_{1)=1。就是說，單位區間內的所有有理數的外容量同單位區間本身的外容量相等。}}}

從某些方面看，這似乎是言之有理的，但從其他方面看，這是有問題的。因為如果我們令I_{1是[0, 1]內的無理數的集合，用完全相同的推理，同樣證明c_e(I_{1)=1。由於不相交的集合Q_{1和I_{1的並集是整個區間[0, 1]，我們看出}}}}

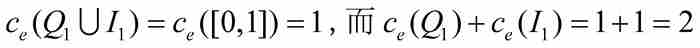
顯而易見，我們不能把一個集合分開成不相交的子集，而它們的外容量之和仍然為原來集合的外容量。這樣的非可加性是哈納克的容量理論不受歡迎的特性。

把長度的概念擴展到非區間集合的這種前景，足以引導其他人修改外容量這樣的定義，以便消除伴隨的問題。許多數學家投身這個討論中，但是歷史把最終解決這個問題的責任賦予勒貝格。如果一個集合「能夠包含在有限個或可數無限個區間內，而這些區間的總長度可以小到我們希望的任意小的地步」，那麼他把它定義為零測度的集合。3 因此，如果對於任意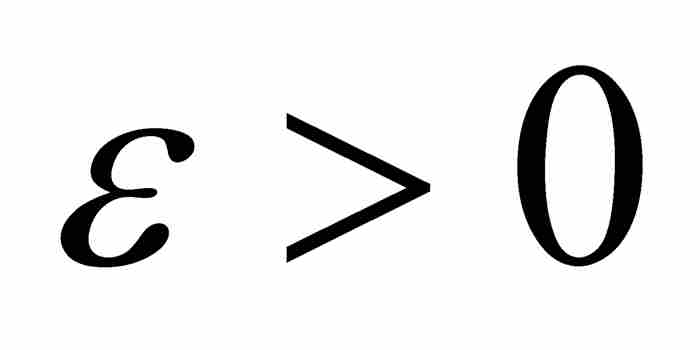，我們能夠使集合E包含在區間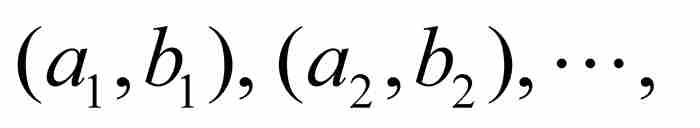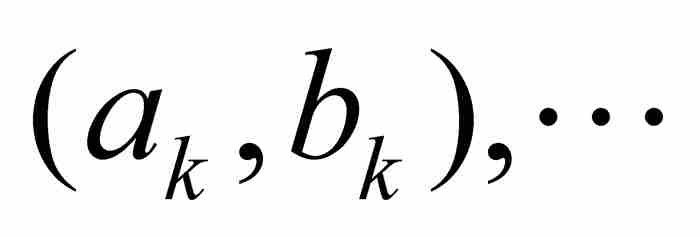內，即

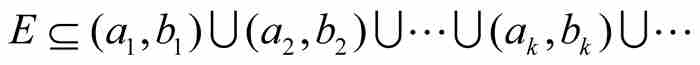
3 Henri Lebesgue, Lecons sur l'integration et la recherche des fonctions primitives, Gauthier-Villars, 1904, p. 28。

其中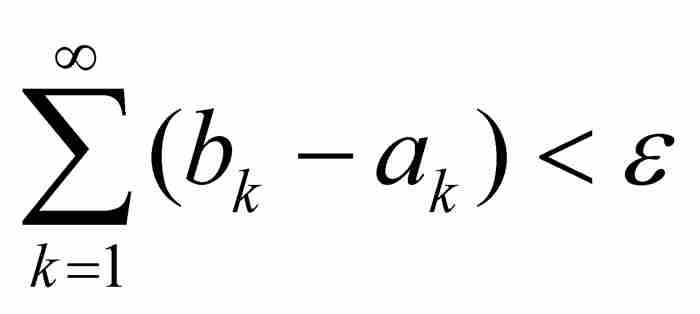，那麼E是零測度的集合，記為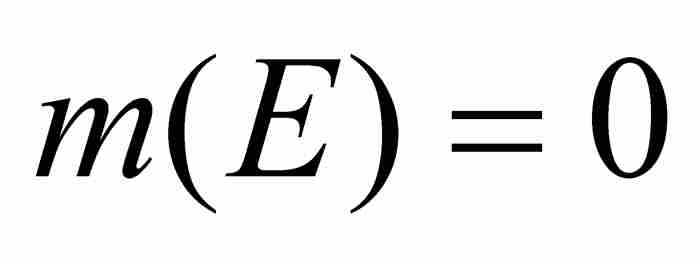。同哈納克不一樣，勒貝格在這裡的創新在於允許用可數無限個區間覆蓋集合，而這樣做同哈納克的做法有天壤之別。

從這個定義明顯看出，一個零測度集合的任何子集必定為零測度集合。同樣明顯，一個外容量為零的集合也具有零測度。因此，單點集合和上面的集合S都是零測度的集合。但是當勒貝格證明下述定理後，證實相反的結論不成立——而且出其不意地不成立。

定理　如果一個集合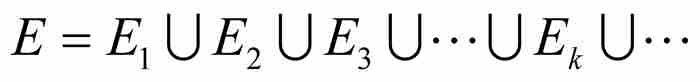是可數個零測度集合的並集，那麼E也是零測度集合。4

4 Henri Lebesgue, Lecons sur l'integration et la recherche des fonctions primitives, Gauthier-Villars, 1904, p. 28。

證明　令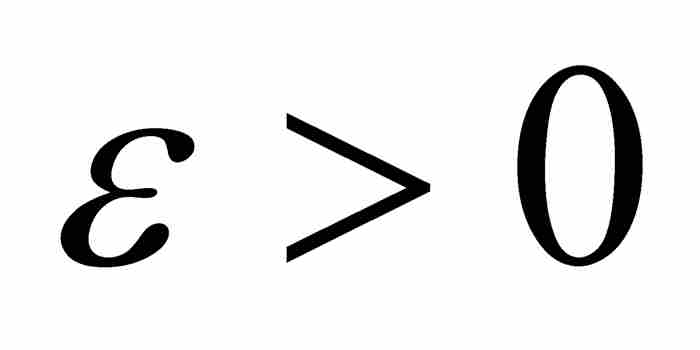是已知的。根據假設，我們可以把E_{1包容在總長度小於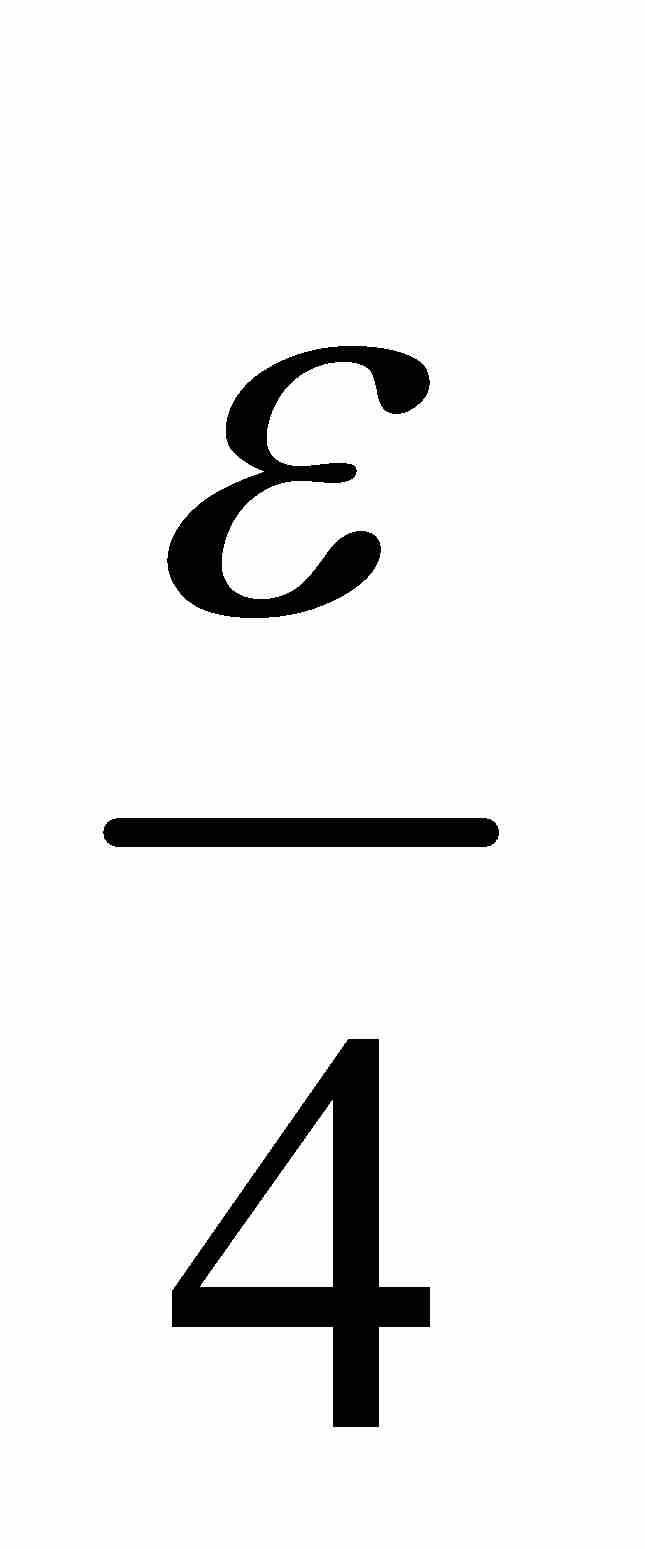的區間的可數集合族內，把E_{2包容在總長度小於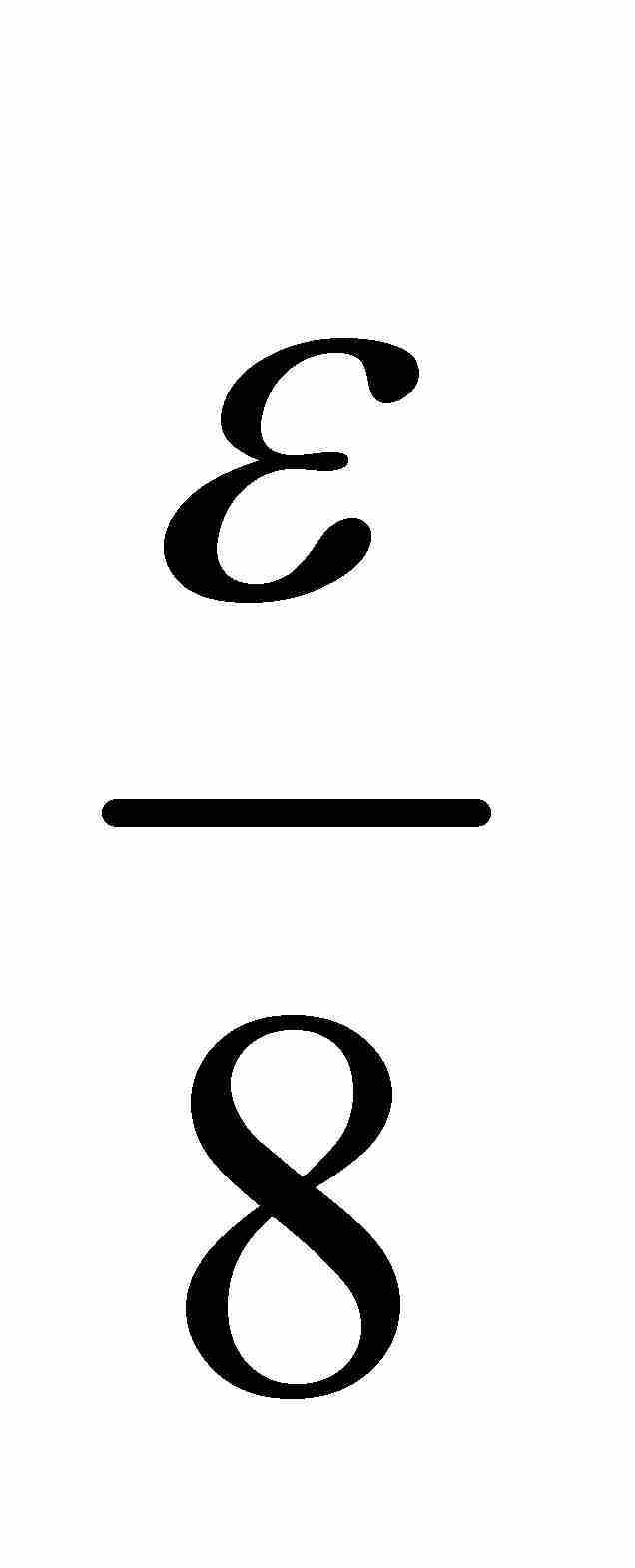的區間的可數集合族內，及至一般情況下，把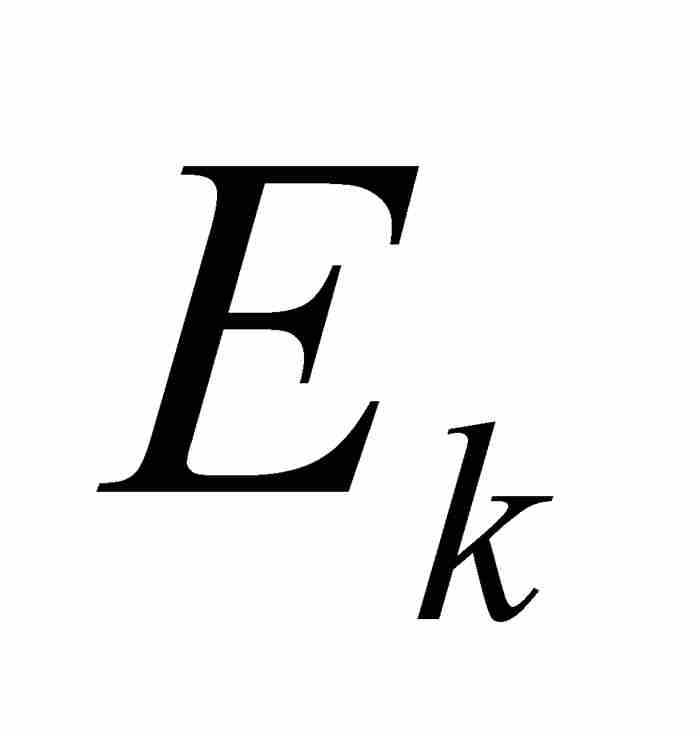包容在總長度小於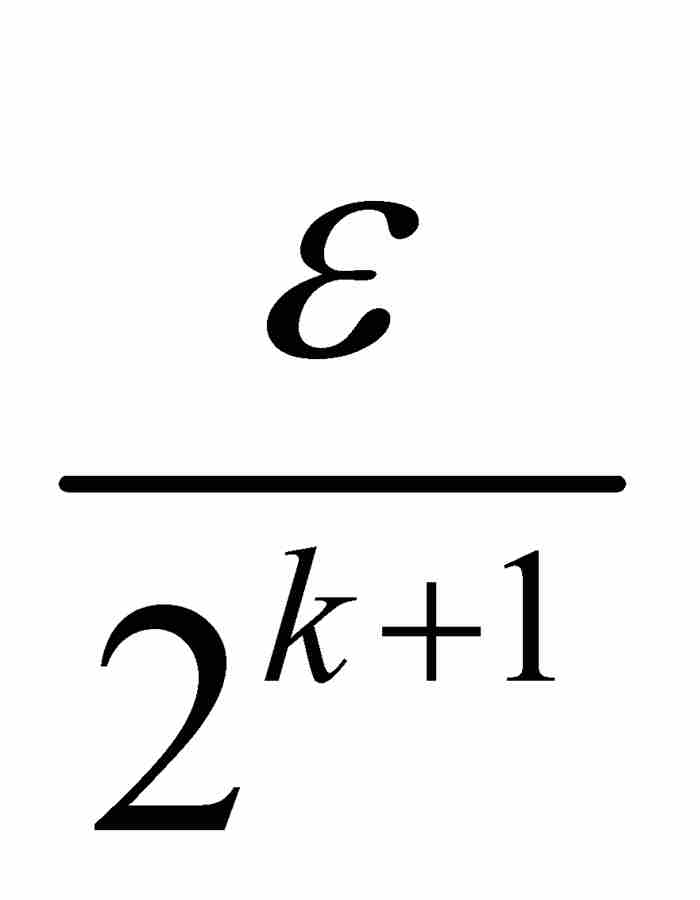的區間的可數集合族內。於是給定的集合E是所有這些區間的並集的一個子集，而這個並集本身作為可數集合族的可數並集是總長度小於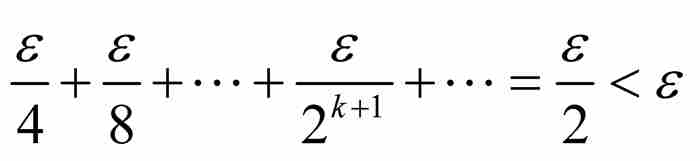的可數集合族。由於E包容在總長度小於任意小的數ε的區間的可數集合族內，可知???具有零測度。}}

由此推出，任何可數集的測度為零，因為這樣一個集合可以表示成它的單個點集的（可數）並集。特別是，區間[0, 1]內的有理數的集合（前面標記為Q_{1的稠密集）具有零測度。由於m(Q_{1)=0，而c_e(Q_{1)=1, 這說明外容度為零與測度為零在根本上是不同的。}}}

為數不多的數學家在具有零測度的稠密集的現象面前可能退縮。畢竟，稠密集是普遍存在的，它會出現在無論多麼小的區間內。哈納克本人在20年之前就開始走上這條道路，但是他把零測度作為可笑的想法拒絕了。5 這樣一種看似非常反常的景象使他相信要堅持採用有限區間的覆蓋。

5 Thomas Hawkins, Lebesgue's Theory of Integration, Chelsea, 1975, p. 64。

但是勒貝格沒有善罷甘休，而當他發現長期尋求的函數的可積性同其連續性點之間的關係時，他證明自己的方法是極有價值的。問題在於，「一個可積函數可能在何等程度上是不連續的？」下面的定理是對於這個問題的簡單回答。

定理　一個有界函數f在區間[a, b]上為黎曼可積的充分必要條件，是它的不連續點的集合具有零測度。6

6 Henri Lebesgue, Lecons sur l'integration et la recherche des fonctions primitives, Gauthier-Villars, 1904, pp. 28-29。

這就是說，勒貝格用條件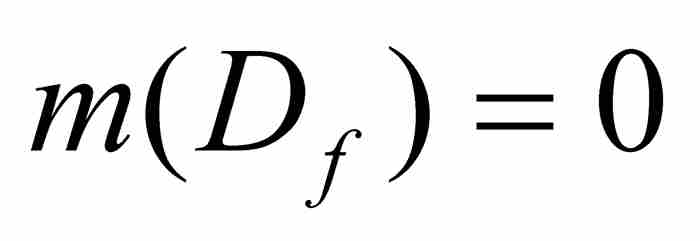填充了句子（2）中的關鍵空白。在許多書籍中把這個定理稱為「勒貝格定理」，說明在他最終證明的大量定理中，這個定理是特別重要的。

毫不奇怪，勒貝格的論證的核心在於黎曼可積條件，這個條件可以改寫如下：函數f在區間[a, b]上是黎曼可積的，當且僅當對於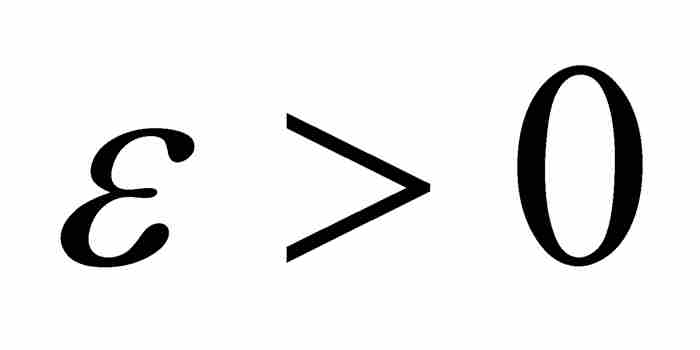任意和任意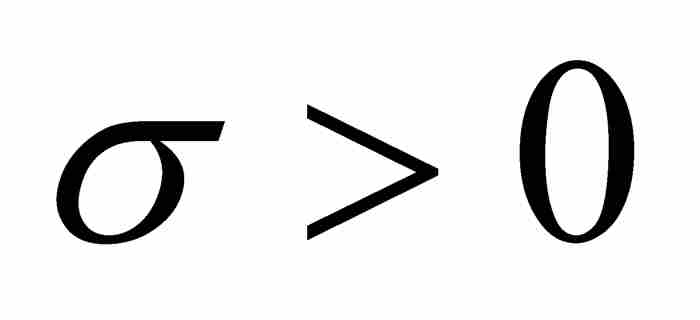，我們可以把[a, b]劃分成有限數目的子區間，其中f的振幅大於σ的點所在的那些子區間（我們稱為A類子區間）的總長度小於ε。

我們注意到，到勒貝格時代，函數在一點的「振幅」的概念比黎曼時代有了更確切的含義。不過就我們的目的而言，依舊可以把它非正式地視為在那個點的鄰域內涵數的最大變差。此外，已經知道，一個函數在點x_{0是連續的充分必要條件是它在x_{0的振幅為零。}}

勒貝格引進G_{1(σ)作為在區間[a, b]中函數f的振幅大於或等於σ的那些點的集合，並且證明G_{1(σ)是一個閉有界集。由於C_f = {x| f在x的振幅為零}，我們知道}}

（3）

等式（3）顯然是成立的。另一方面，在任何不連續的點，振幅必定為正，因此對於某個自然數N，其值超過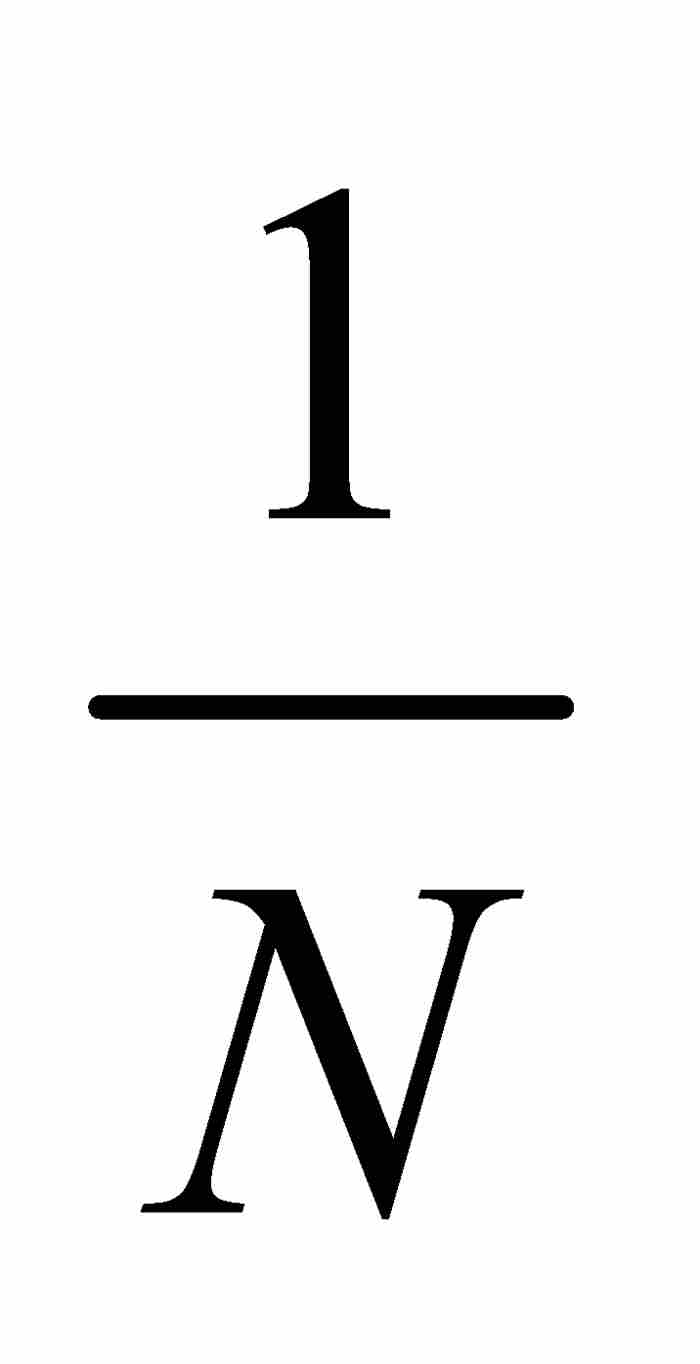。這意味著不連續的點屬於G_{1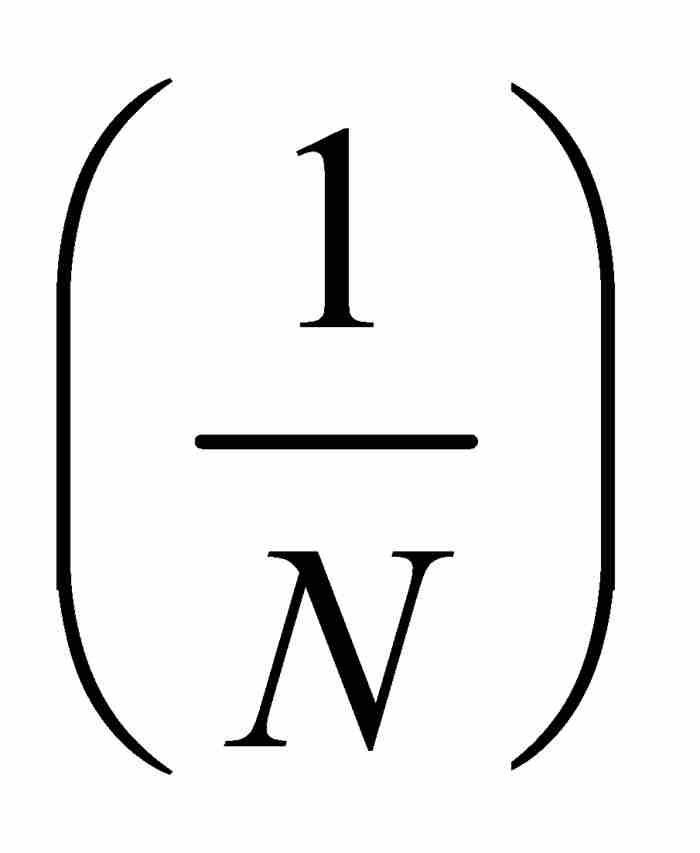，因此屬於等式（3）右端的並集。反過來說，這個並集中的任何點必定屬於某個G_{1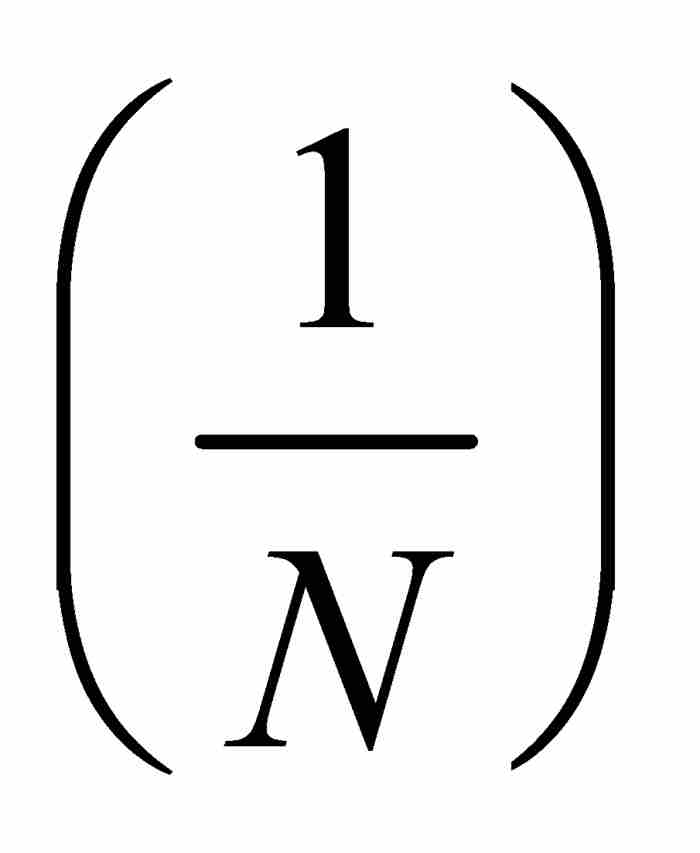，因此有一個正振幅使它成為一個不連續的點。}}

在這種背景下，我們來考察勒貝格的證明。

證明　首先假定有界函數f在區間[a, b]上是黎曼可積的。對於任何自然數k，可積性條件保證振幅大於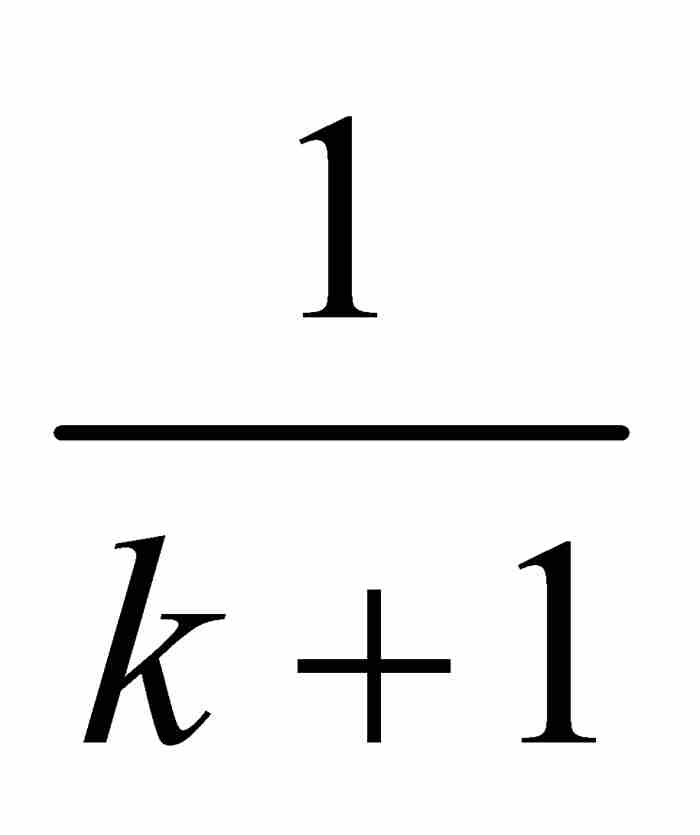的點的集合可以包容在有限個區間內，這些區間的總長度小到我們希望的任意小。因此這個集合以及它的子集G_{1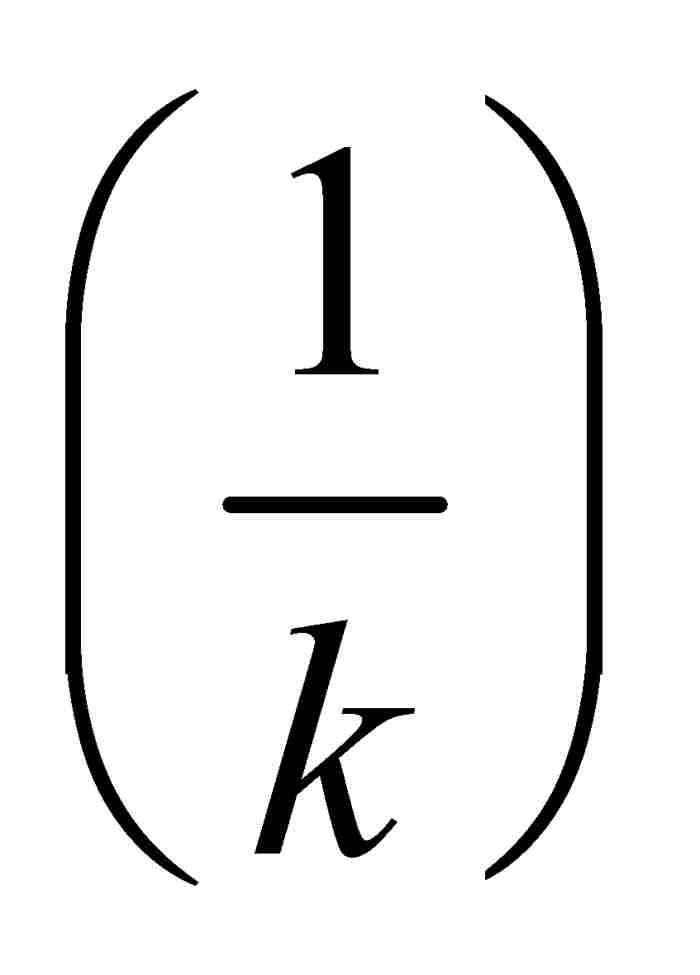的外容量為零，所以G_{1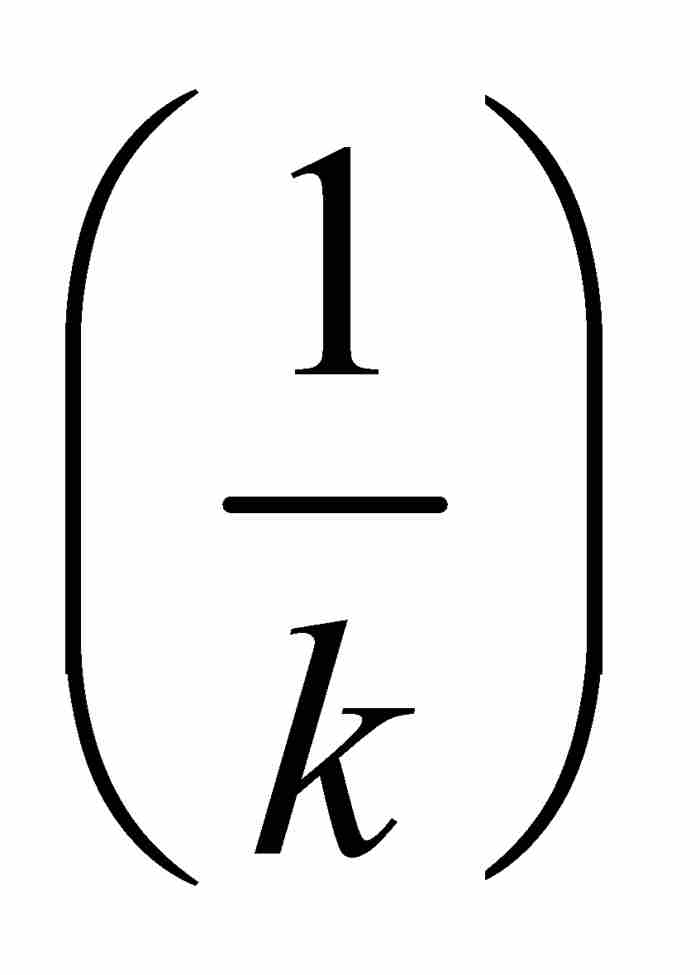具有零測度。根據前面的定理，並集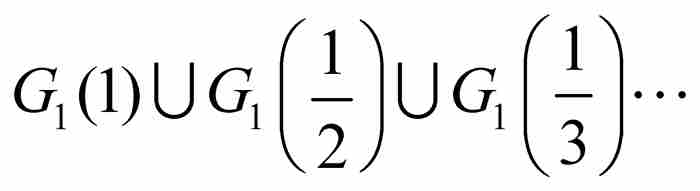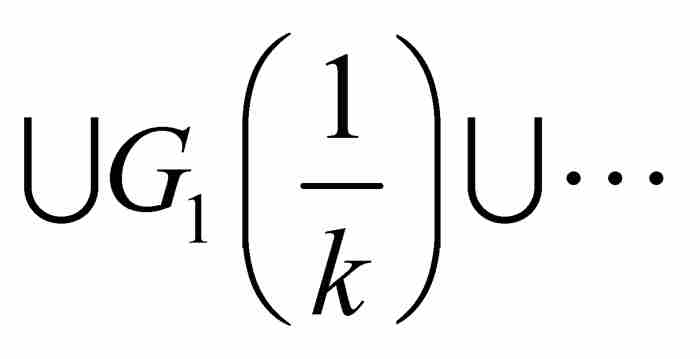是零測度的集合，由式（3），這蘊含D_f也是零測度的集合。這就完成必要條件的證明。}}

為了證明充分條件，假定m(D_f)=0，並且令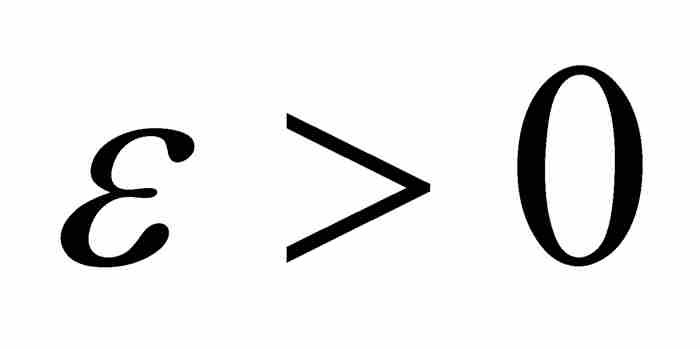和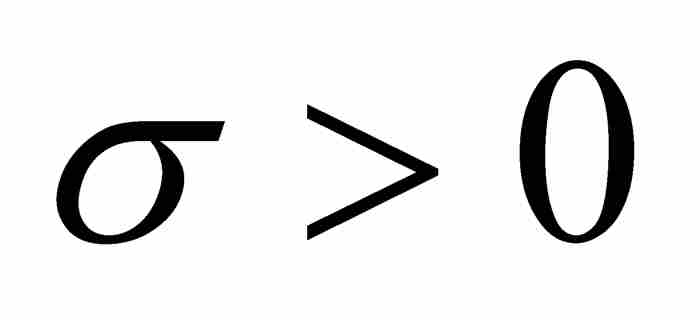。選擇一個滿足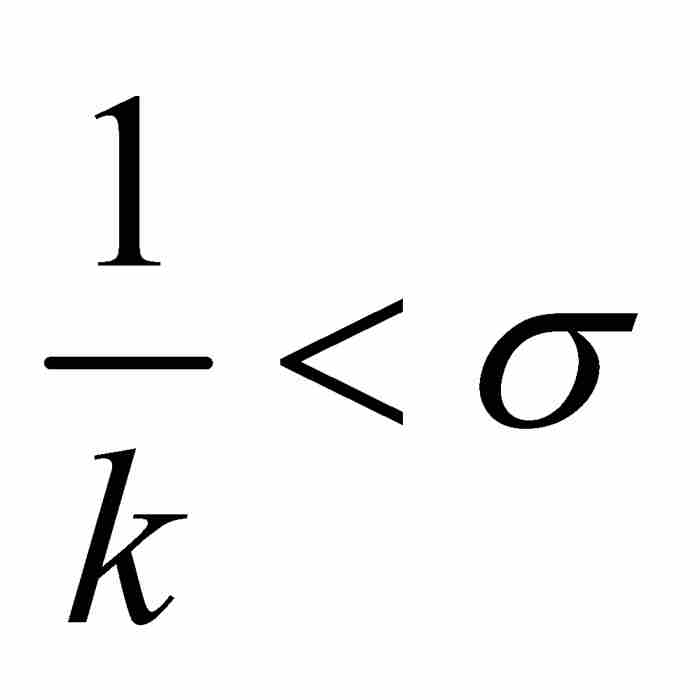的自然數k。於是函數f的振幅超過σ的點的集合是G_{1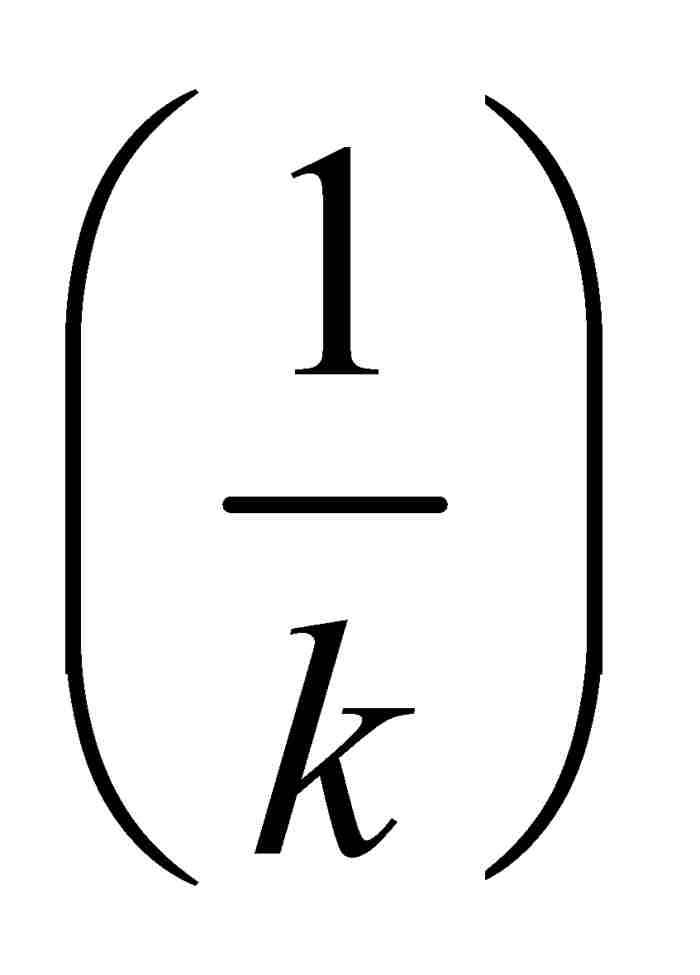的一個子集，它也是D_f的一個子集。因此，G_{1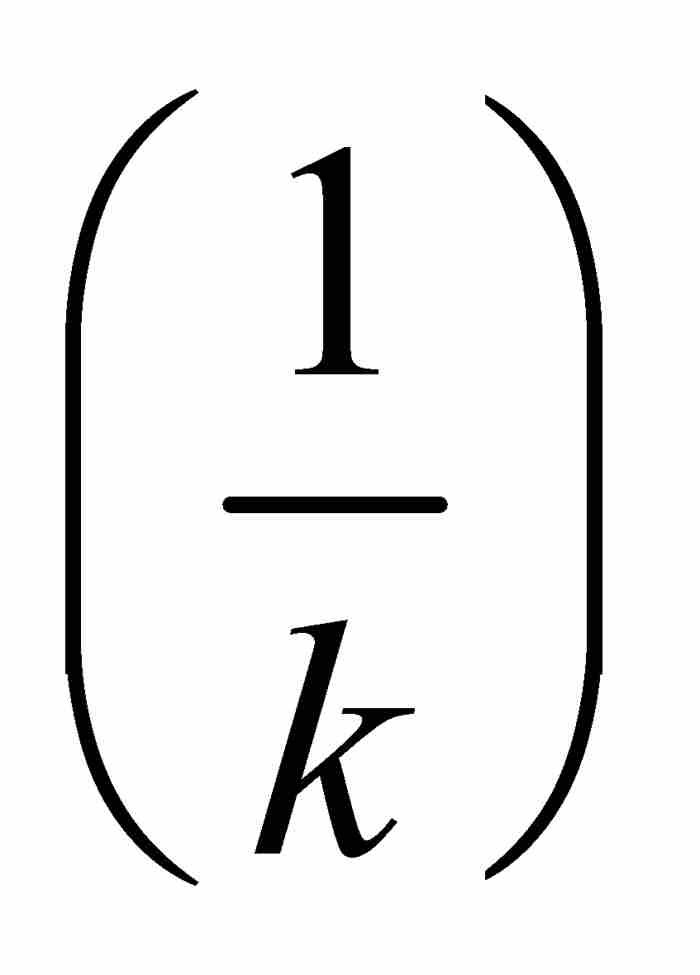是零測度的集合，所以能夠包容在總長度小於ε的（開）區間的可數集合族內。由於G_{1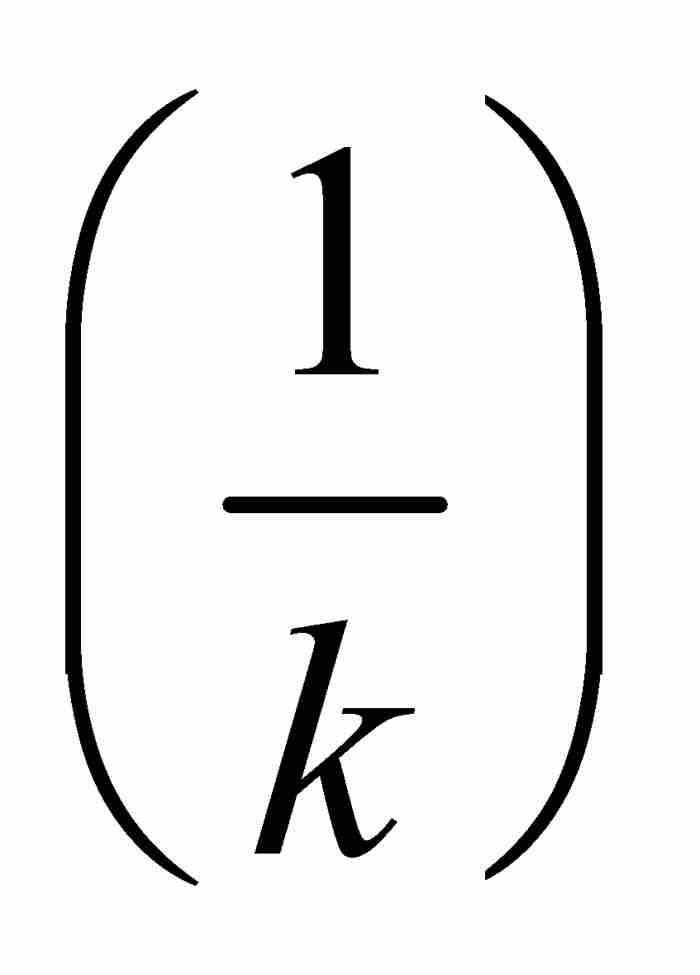是閉集和有界集，勒貝格可以應用著名的海涅—波雷爾定理推斷，G_{1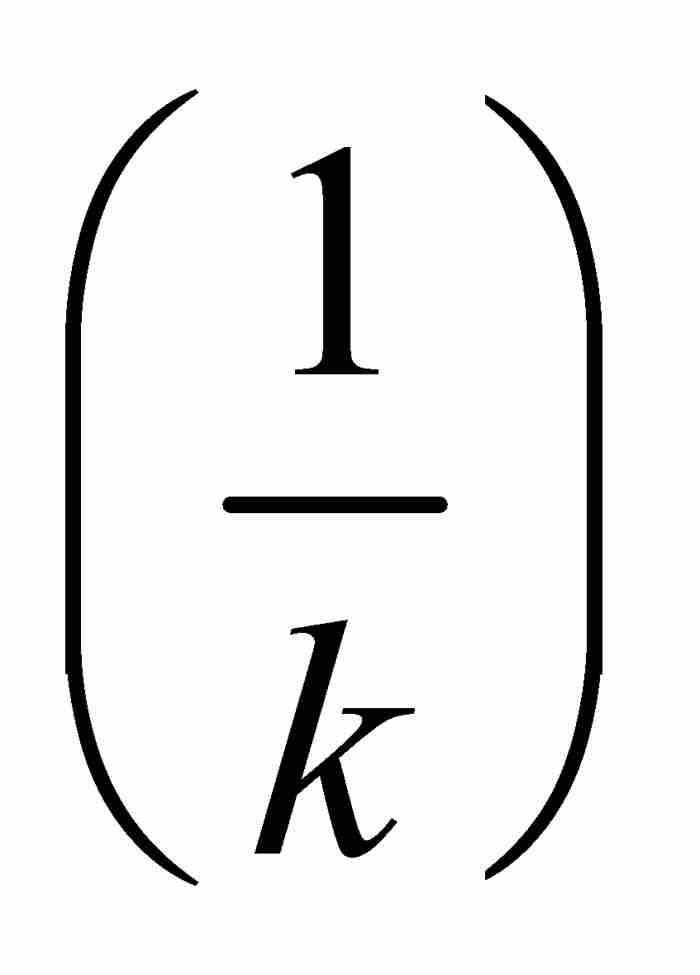位於這些開區間的一個有限子集合族內7。這個有限的子集合族的總長度顯然小於ε，並且不僅覆蓋G_{1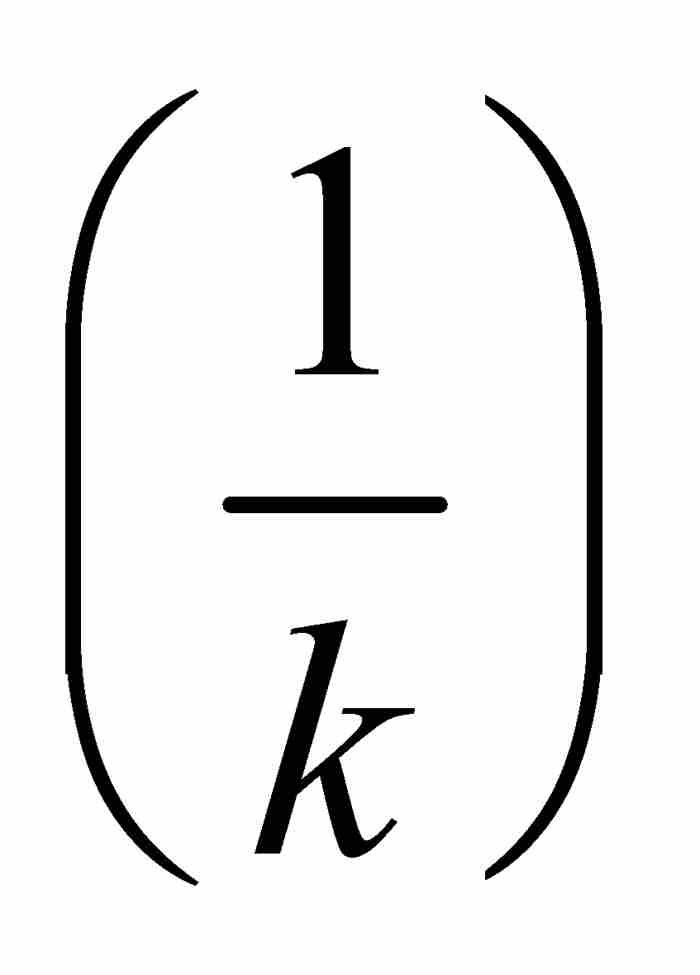，而且覆蓋更小的振幅超過σ的點的集合。總之，可積性條件是滿足的，所以f是黎曼可積的。}}}}}

7 實數的閉有界集的海涅—博雷爾定理是任何分析學教科書討論的一個主題；例如參閱Frank Burk, Lebesgue Measure and Integration, Wiley, 1998, p. 65。它的歷史是錯綜複雜的，但是我們注意到，在勒貝格的論文的104~105頁包含一個精彩的證明，這是他的著名學位論文中的另外一個重點。其他資料請參閱Pierre Dugac, 「Sur la correspondance de Borel et le theoreme de Dirichlet-Heine-Weierstrass-Borel-Schoenflies-Lebesgue,」 Archives internationales d'histoire des sciences , 39 (122) (1989), pp. 69-100。

此後，勒貝格定義了函數的一種幾乎處處具有的性質，這是指函數只在零測度集上不保持的性質。用這個術語，我們把勒貝格定理簡潔地重述如下：一個有界函數f在區間[a, b]上是黎曼可積的，當且僅當它是幾乎處處連續的。

這個特徵非常有用，例如，我們可以用它立刻證明[0, 1]上的直尺函數R的可積性。正如我們曾經證實的那樣，R在除測度為零的有理數集之外是連續的。這意味著直尺函數是幾乎處處連續的，所以是黎曼可積的。

在數學分析中，勒貝格定理堪稱一個經典。從所發生的事情來看，帶有幾分諷刺意味的事實是，徹底瞭解黎曼積分的人正是使它不久就變得陳舊的人：這就是勒貝格。

集合的測度

零測度概念的全部重要性在於僅對實直線上的某些集合是適用的。勒貝格在他的論文中繼續對一個大得多的集合族定義了「測度」。基本思想是從他的同胞埃米爾·博雷爾（1871—1956）那裡借用來的，但是勒貝格對它所做的改進是無法測度的（我們敢相信嗎？）。

這個方法有一個我們熟悉的環節。對於一個集合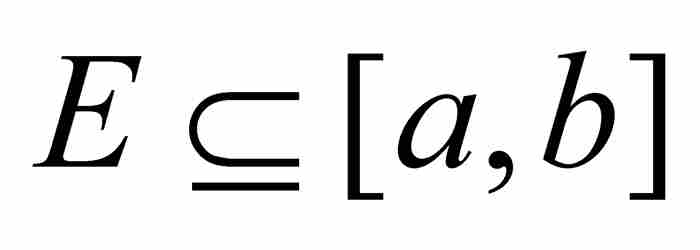，勒貝格寫道：

我們可以把它的點包容在有限的或者可數無限的區間內，這些區間的點集的測度是……它們的長度的之和，這個和是E的測度的一個上界。所有這種和的集合有一個下極限m_e(E)，就是E的外測度。1
1 Henri Lebesgue, Lecons sur l'integration et la recherche des fonctions primitives, Gauthier-Villars, 1904, p. 104。

用符號表示，這相當於

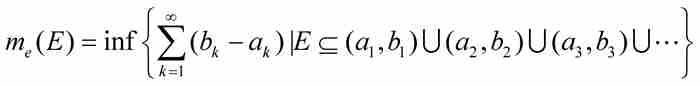
其中我們用到了所述集合的下確界或最大下界。此外，外測度同外容量之間的差別，在於勒貝格除了考慮有限的覆蓋之外還考慮到可數無限的覆蓋。他立刻注意到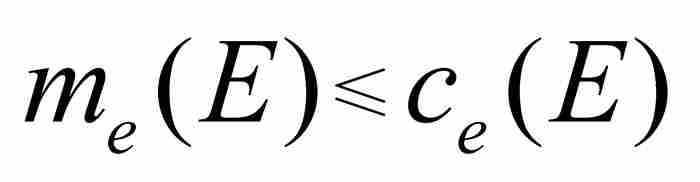，因為取更多的覆蓋僅有可能降低它們的最大下界。

接著他考查了E在[a, b]內的補集，我們把它表示成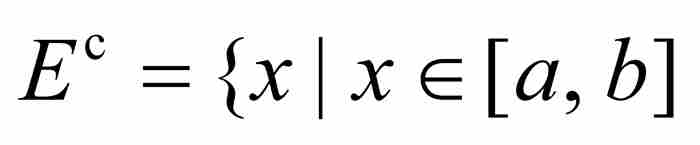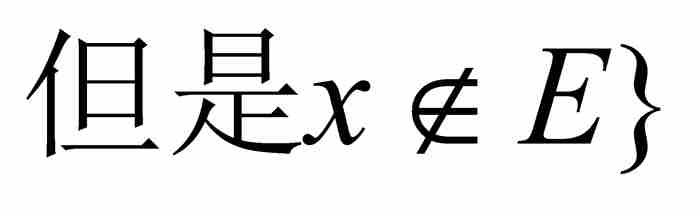，。用上述定義，他求出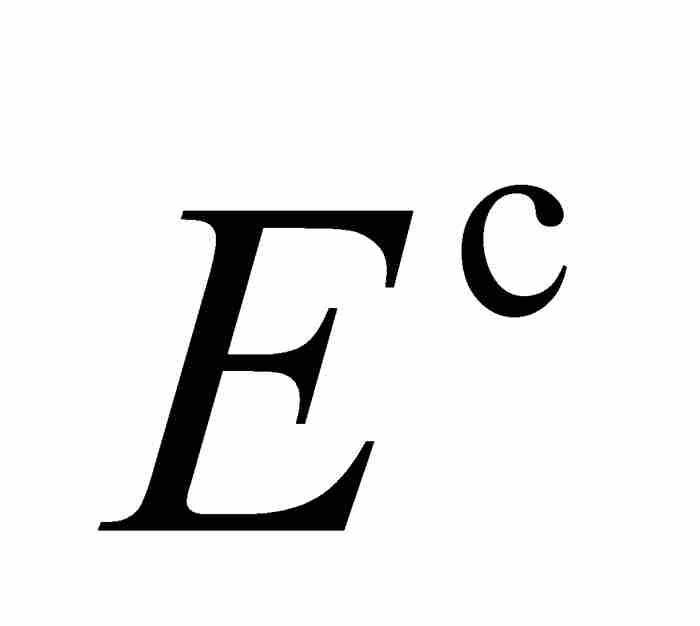的外測度，然後把E的內測度定義為。

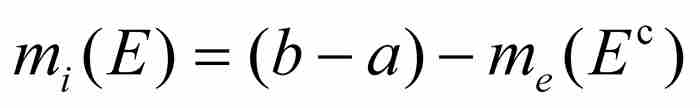一種現代處理方法不用E的補集的外測度去確定它的內測度，而改用有限個或者可數無限個區間的並集從內部「填充」集合E，然後取它們的長度之和的最小上界或者上確界。就是說

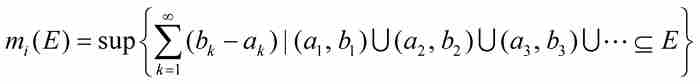
對於有界集而言，這兩種方法是等價的，但是第二種方法同樣也適用於E為無界集的情形。

這時勒貝格證明了「內測度不會大於外測度」，就是說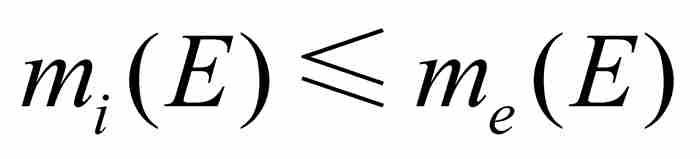，，並且接著提出關鍵性定義：「內測度和外測度相等的集合稱為可測的，而它們的測度為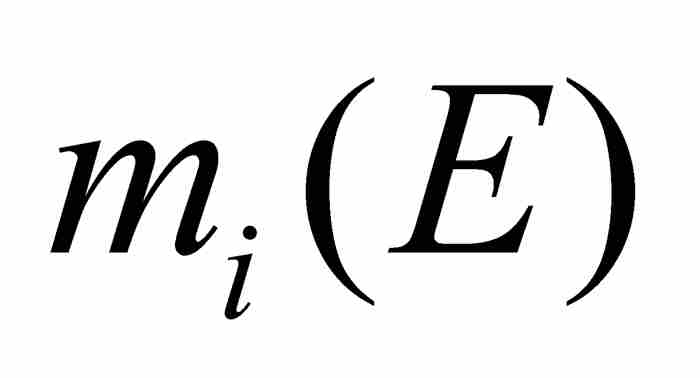和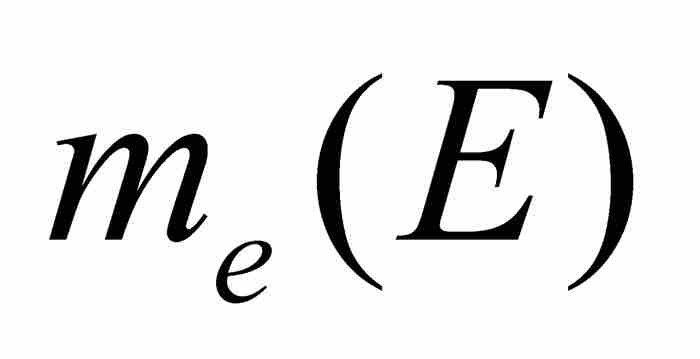的共同值。」 2

2 Henri Lebesgue, Lecons sur l'integration et la recherche des fonctions primitives, Gauthier-Villars, 1904, p. 106。

可測集是一個千真萬確的龐大家族，它包括任何區間，任何開集和閉集，任何零測度集，以及有理數集和無理數集。事實上有過一段時間，數學家們未能找到一個不是可測的集合，即一個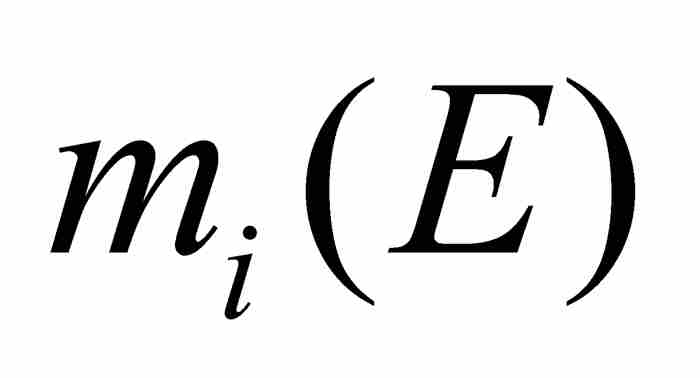<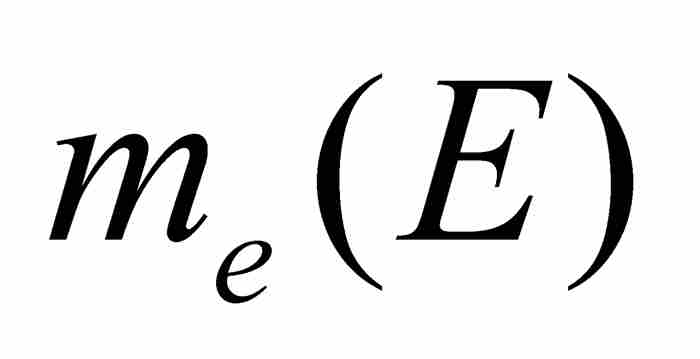的集合。這樣一些集合最終是通過選擇公理構造出來的，而其結果是極端複雜的。3

3 Frank Burk, Lebesque Measure and Integration, Wiley 1988, pp. 266-272。

勒貝格仔細研究了從他的定義得出的結果，其中最基本的三個結果如下。

如果E是可測的，那麼。

一個區間的測度是它的長度。

如果E_{1, E_{2, E_{3, …, E_k,…是有限的或者可數無限的兩兩不相交的可測集，並且如果是它們的並集，那麼E是可測的，同時。}}}

第三個結果是外容量所不具備的可加性性質。我們用它可以輕而易舉地求出區間[0, 1]內無理數的集合的測度，這個集合就是上面所說的I_{1。我們注意到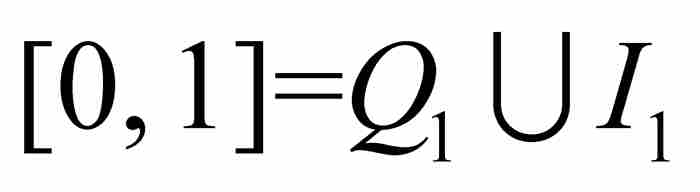，，其中右端的兩個集合是不相交的和可測的。因此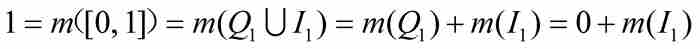，，所以m(I_{1)=1。就測度而言，無理數在[0, 1]中處於支配地位，而有理數是無足輕重的。}}

勒貝格測度尤其在「小型」集合（零測度）和「大型」集合（正測度）之間提供一種新的一分為二的方法。本書把這種方法同用基數的一分為二的方法（可數集與不可數集）和拓撲的一分為二的方法（第1類集合與第2類集合）相提並論，在所有這三種分法中，有理數的集合都被看作小型集合，因為它們是零測度的和可數的，是屬於第1類的集合，而無理數的集合是大型集合，它們是正測度的和不可數的，是屬於第2類的集合。

繼續採用這種觀點，我們看出在所有這三種一分二的方法中，「小型」集合的子集和可數並集仍舊是「小型」集合，並且我們證明了一個可數集既是第1類的集合，又是零測度的集合。但是，其他「大型」和「小型」集合之間的聯繫不復存在。有可能找到第1類集合，它們是非可數的和正測度的集合，同時找到零測度集合，它們是非可數的和屬於第2類的集合。4 很明顯，這些概念已經使數學家們陷入某種困境。

4 參閱Bernard Gelbaum and John Olmsted, Counterexamples in Analysis, Holden-Day, 1964, p. 99。

在勒貝格的博士論文中，他不滿足於僅考慮可測集。他定義了如下的可測函數：一個有界的或非有界的函數f，如果對於任何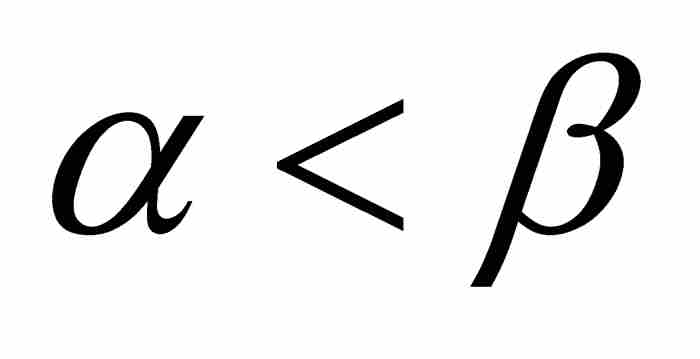，集合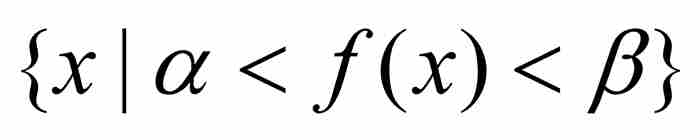是可測的，我們就說它是可測函數。5 圖14-2給出這個定義的幾何意義。對於沿y軸的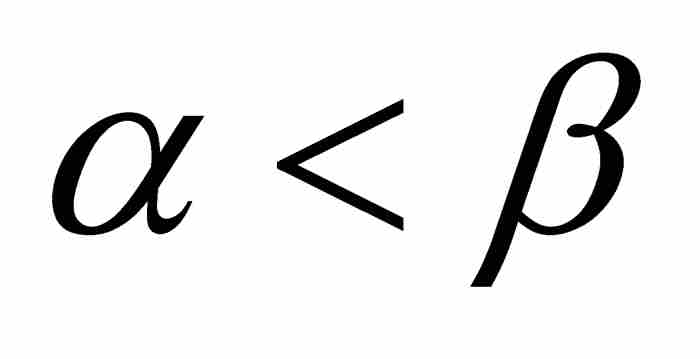，我們把定義域內涵數值介於α和β之間的所有x點彙集起來，如果這個集合對於α和β的所有選擇都是可測的，就說f是可測函數。

5 Henri Lebesgue, Lecons sur l'integration et la recherche des fonctions primitives, Gauthier-Villars, 1904, p. 111。

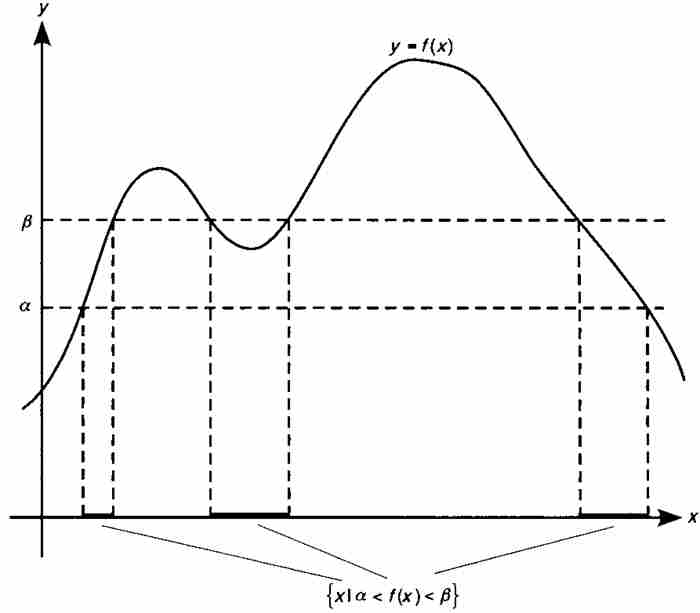
圖　14-2

利用可測集的性質，勒貝格證明了f是可測函數，當且僅當對於任何α，集合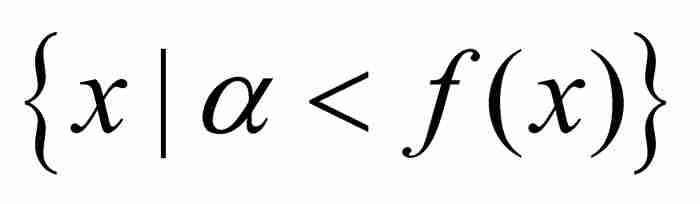是可測的。從這個結果很容易推出狄利克雷函數是可測的，因為對於集合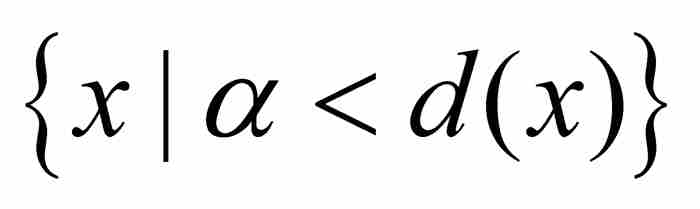僅有三種可能性：如果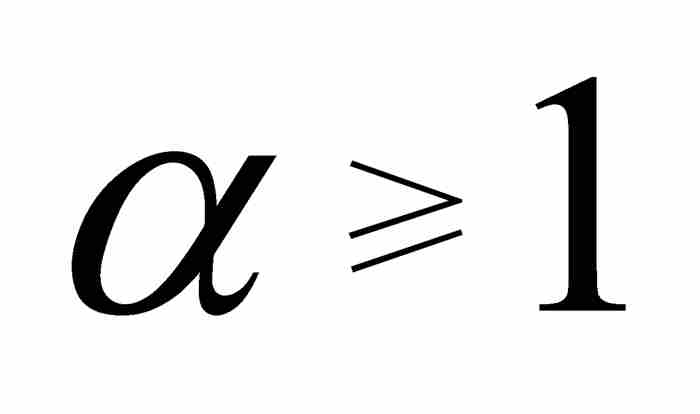，它是空集；如果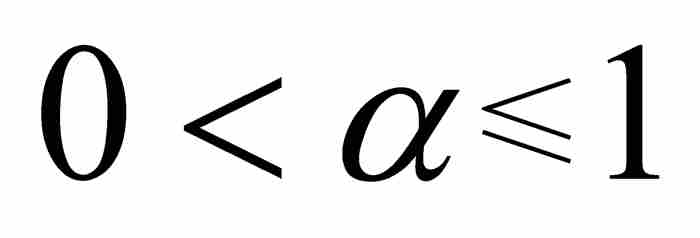，它是有理數集；如果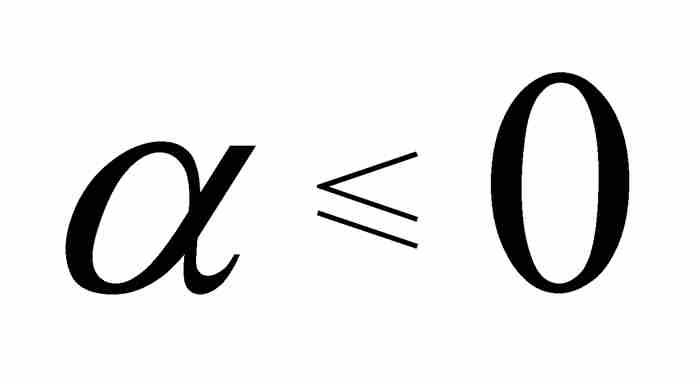，它是全部實數的集合。在每種情形下，這些集合都是可測集，所以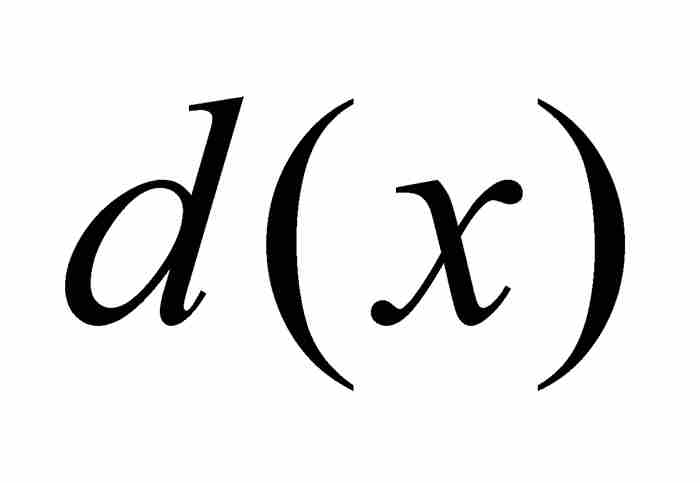是一個可測函數。

我們已經見過，狄利克雷函數既不是點態不連續的，也不是黎曼可積的。由於它的原始特性，被排除在這兩個函數族之外。但是它是可測的。人們開始意識到，通過引進可測函數，勒貝格已經撒下了他的天網。

他沿著他的推理路線繼續前進，證明對於一個可測函數f而言，集合

，，

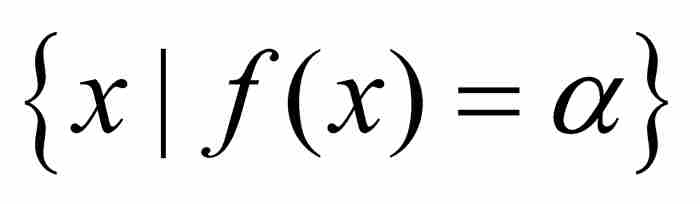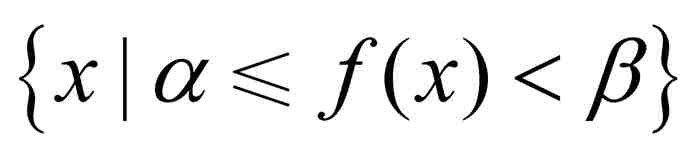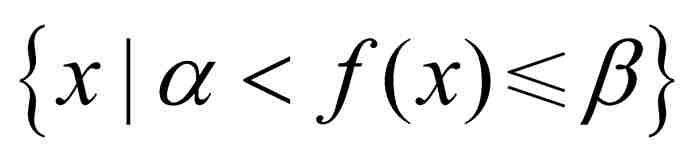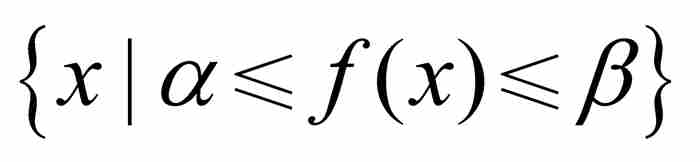和（4）

都是可測集。他還證明，兩個可測函數的和與積是可測函數，這意味著我們不能憑借加法和乘法跳出可測函數的範圍。「但是，」勒貝格寫道，「還有下面的結果。」

定理　如果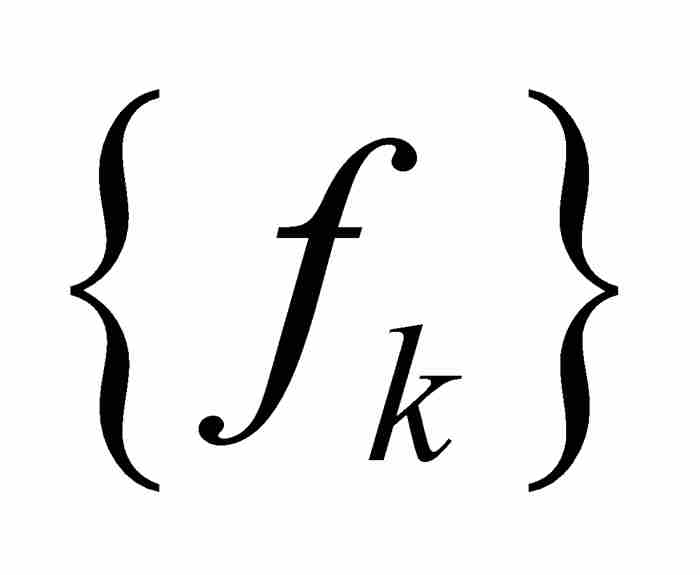是一個可測函數的序列，而且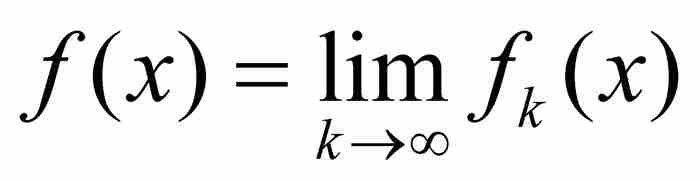是它的點態極限，那麼f也是可測函數。6

6 Henri Lebesgue, Lecons sur l'integration et la recherche des fonctions primitives, Gauthier-Villars, 1904, p. 111。

這是值得注意的，因為這個定理表明，我們甚至也不能通過取點態極限逾越可測函數的範圍。從前面式（1）中我們曾經見過，這對於有界的黎曼可積函數是不真實的，而且我們在前面幾章指出過，這對於連續函數或者那些屬於貝爾的第1類函數同樣是不可能的。在那些情況下，函數族的限制過於嚴格以至不包含它們的所有點態極限。對比之下，可測函數是明顯包含點態極限在內的。

勒貝格很快指出這幾個定理的一個令人著迷的推論。我們可以毫不費力地看出，常值函數是可測的，恆等函數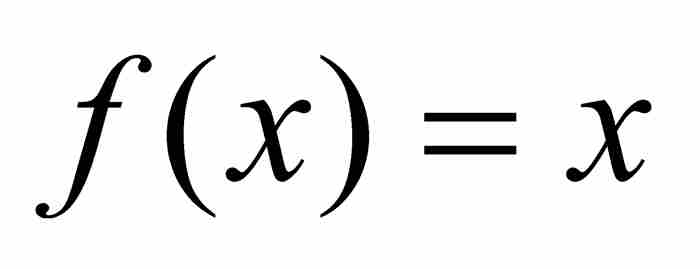同樣是可測的。再通過函數的相加和相乘，可知任何多項式函數是可測的。魏爾斯特拉斯逼近定理（見第9章）保證，區間[a, b]上的任何連續函數是一個多項式序列的一致收斂極限，所以根據上述定理，任何連續函數是可測的。由於同樣理由，連續函數的點態極限是可測的，然而這些函數只不過是貝爾的第1類函數。這表明可微函數的導數是可測的。同時，貝爾的第2類函數，像狄利克雷函數，也是可測的，因為這些函數是貝爾的第1類函數的序列的點態極限。同樣的推理揭示，每一個貝爾類中的任何函數都是可測的。

完全可以說，在1900年以前考察過的任何函數都屬於勒貝格可測函數族。這是一個千真萬確的龐大家族。

然而，從某種意義上說，所有這一切只是一個序幕，勒貝格正準備利用可測集和可測函數的思想作出他的最大貢獻。

勒貝格積分

有界函數f的黎曼積分從把定義域剖分為細小的子區間的一個劃分開始，在這些子區間上構建矩形，它們的高由函數值確定，最後令最大子區間的寬度收縮為零。相反，替代的勒貝格積分乃是基於一種簡單而又富有想像力的思想：採用函數值域的劃分代替定義域的劃分。

我們用圖解來說明，考慮圖14-3中的有界可測函數。勒貝格令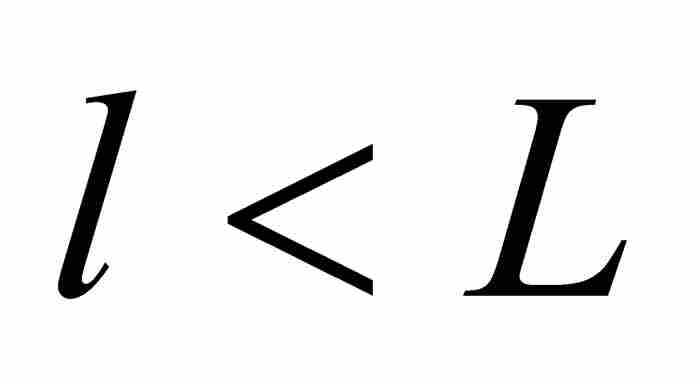為f在區間[a, b]上的下確界和上確界，即函數的最大下界和最小上界，所以區間[l, L]包含函數的值域。於是，對於任意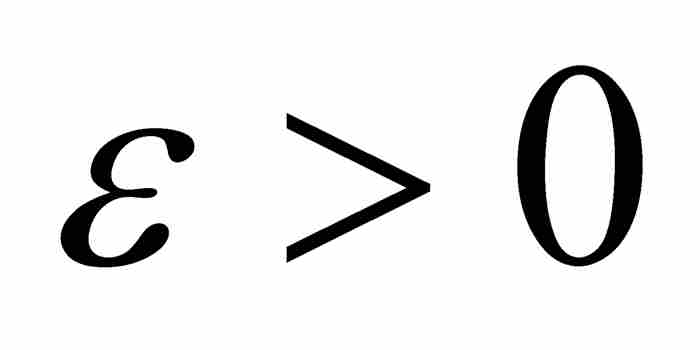，勒貝格設想區間[l, L]的一個由點

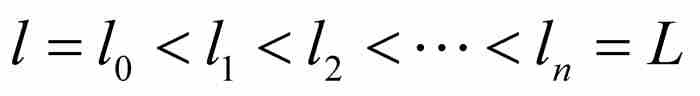
構成的劃分，其中相鄰分點之間的最大間隔小於ε。

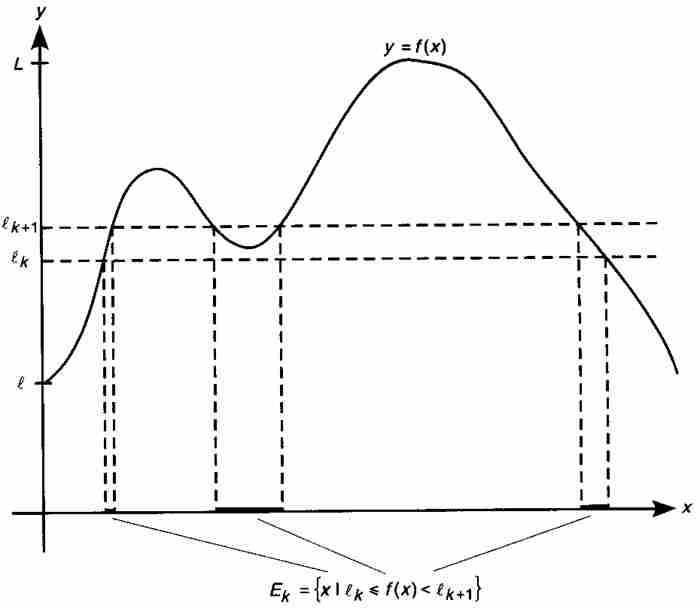
圖　14-3

用沿y軸的這樣一個劃分，我們建立「勒貝格和」。像黎曼和一樣，我們將用面積已知的一些區域逼近曲線下方的區域，不過我們可以不再要求這些區域一定為矩形。相反，我們考慮沿y軸的子區間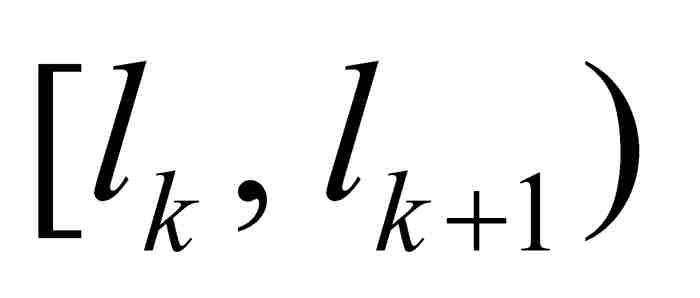，並且注意由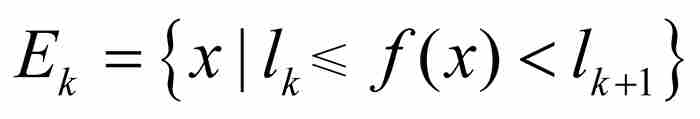定義的[a, b]的子集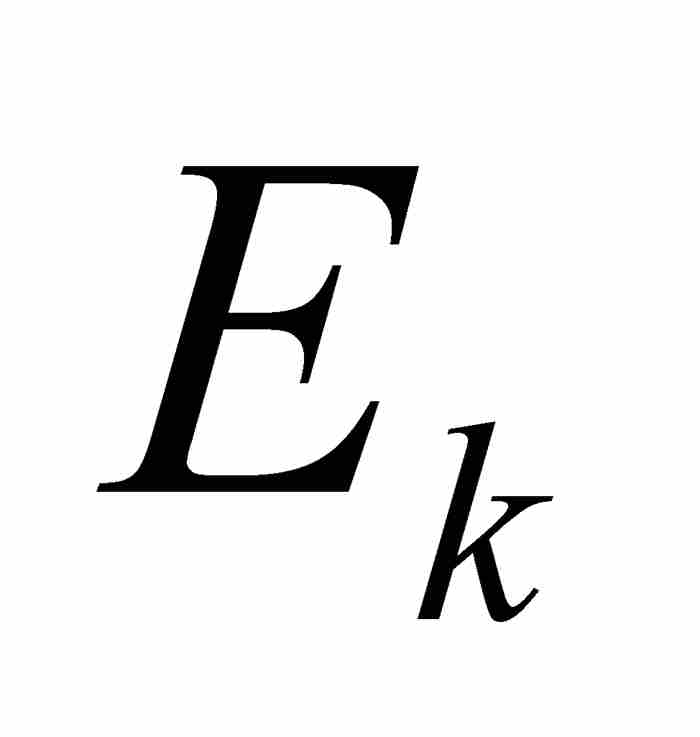。這個子集就是圖14-3中在x軸上標示出的部分。這裡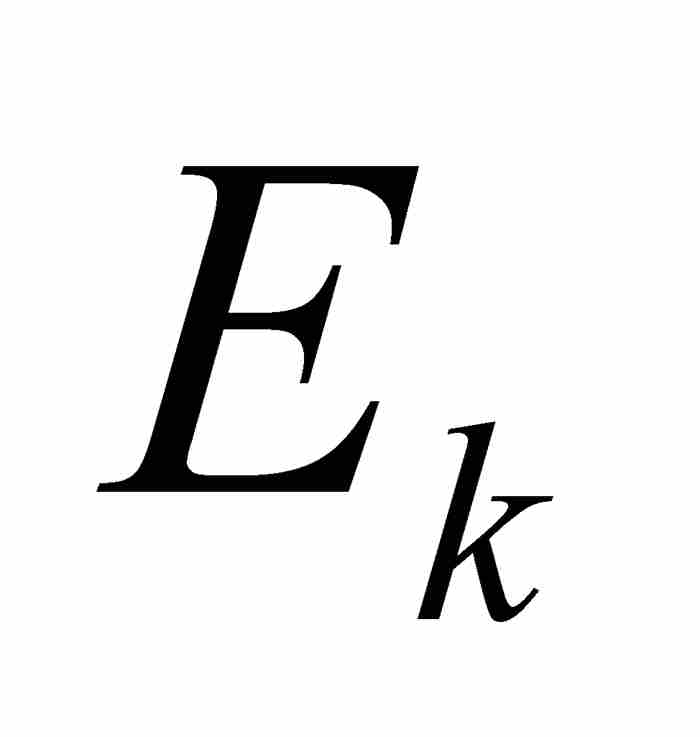，是三個子區間的並集，但是它的結構可能非常複雜，這同求積分的函數有關。

在黎曼方法的相似步驟中，我們是構造一個矩形，它的高是函數值的近似值，寬是相應子區間的長度，而其面積為這兩個值的乘積。對於勒貝格積分，我們用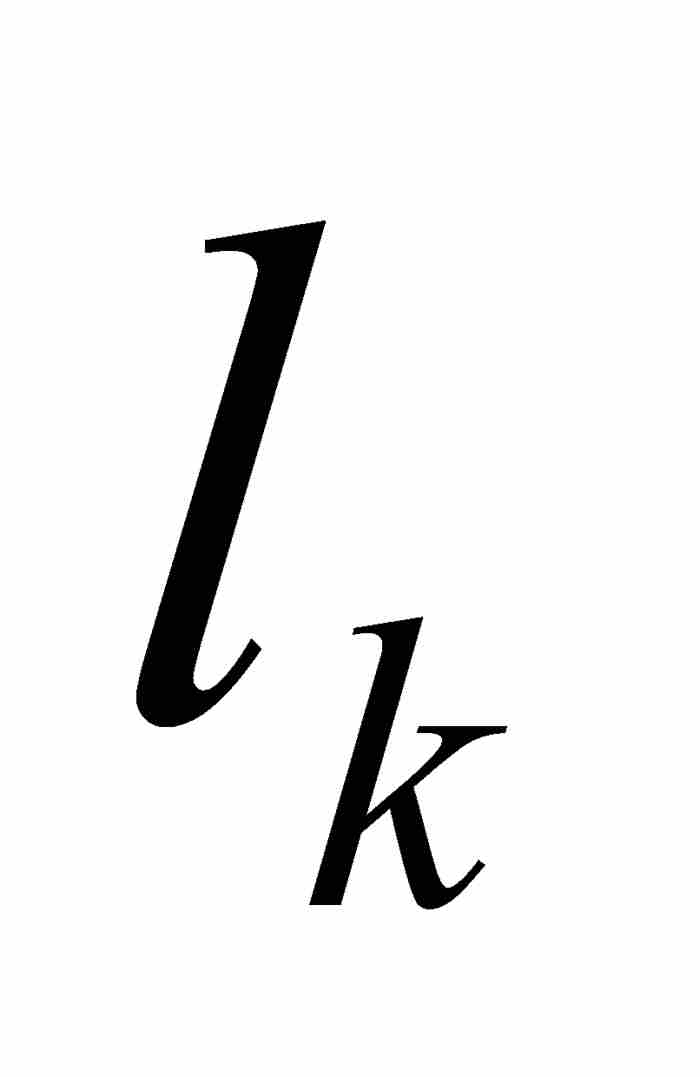作為函數在集合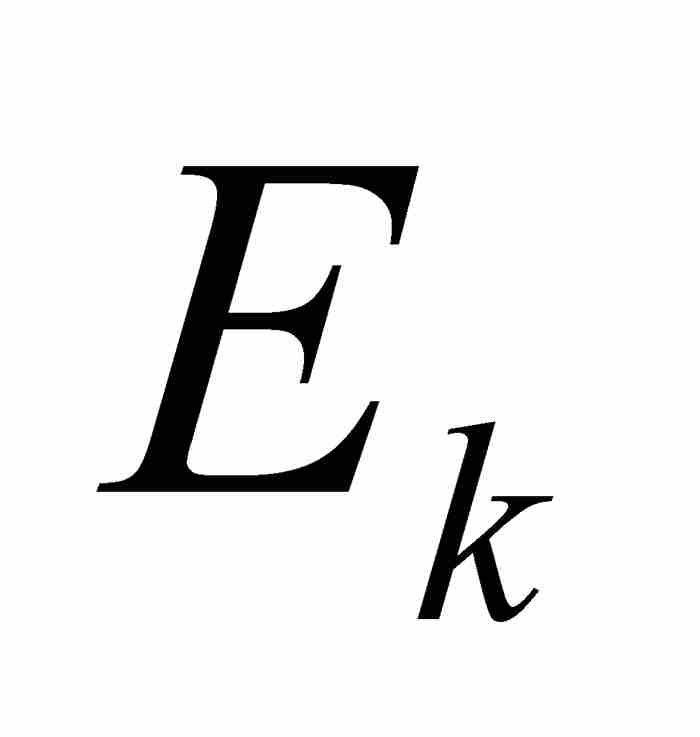上的近似值，但是如果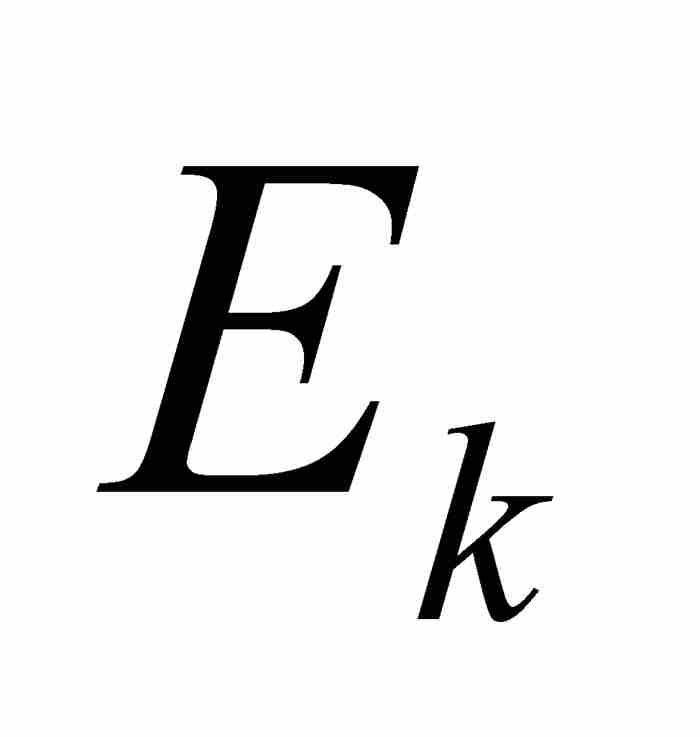不是區間的情形，如何去確定它的長度呢？

毫不奇怪，答案是用集合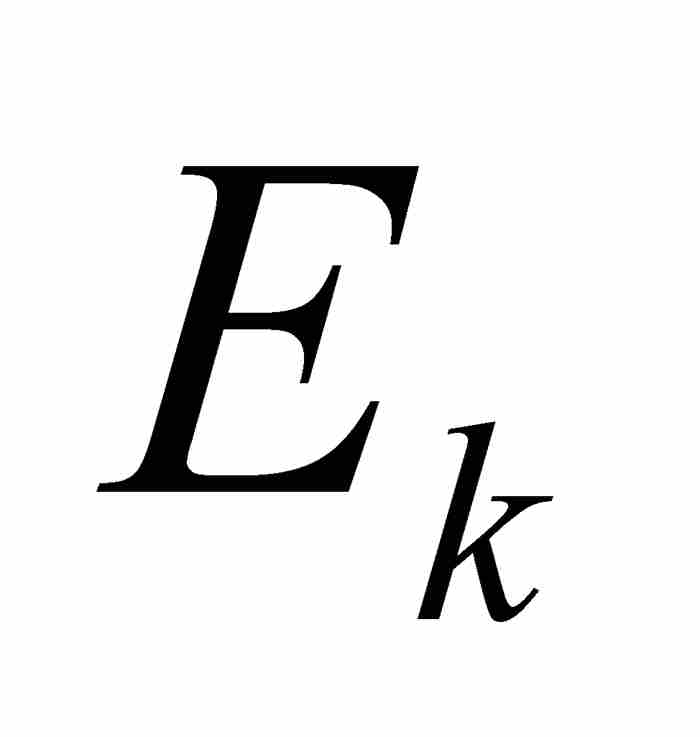的測度扮演這種長度的角色。我們用高乘「長度」得到的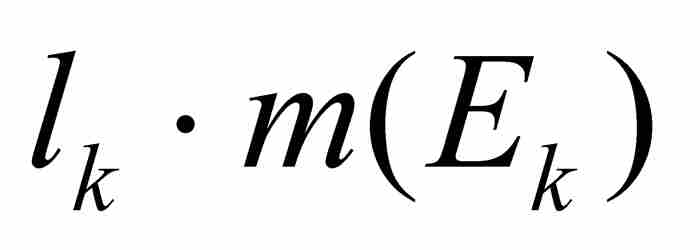作為黎曼和中窄小矩形之一的相應面積。在函數值域的所有子區間上對這些面積求和，我們得到一個勒貝格和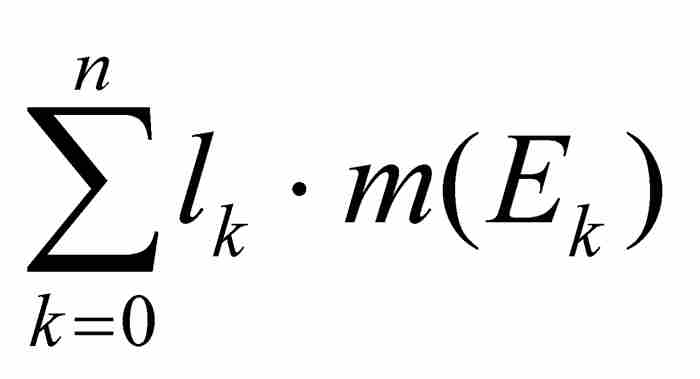，在這個級數中我們令最後一項為。最後，勒貝格令，致使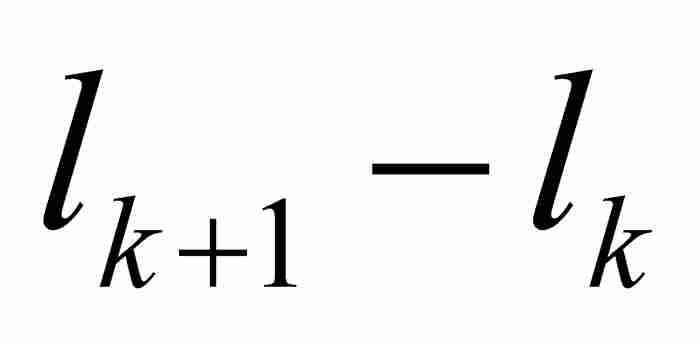的最大值也趨近零。如果通過極限過程產生一個唯一的值，我們就說f在[a, b]上是勒貝格可積的，並且定義

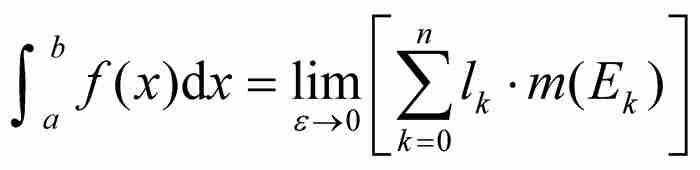
在繼續進行討論之前，我們必須說明兩個問題。第一，很明顯，集合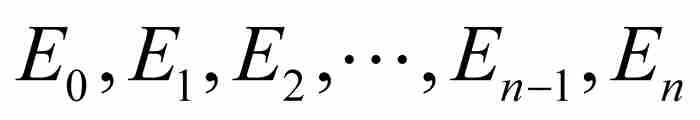把區間[a, b]劃分成若干子集，不過不一定是子區間。第二，我們假定f是可測的，根據式（4），這個假定蘊含每個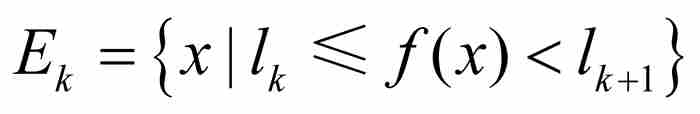以及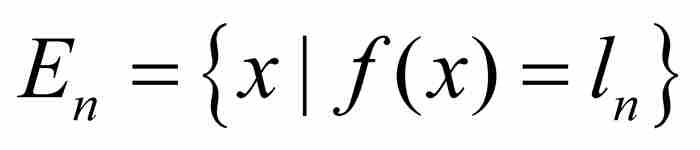是可測集，所以我們完全可以討論關於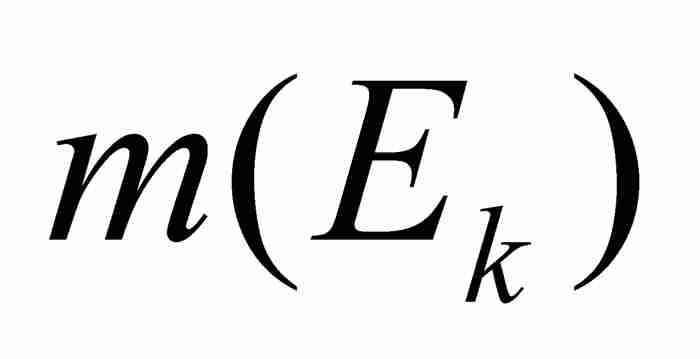的問題。至此，一切都井然有序。

勒貝格在為一般讀者編寫的一本書中，用一個比喻來對比黎曼的方法與他自己的方法。1他想像一位零售商，在一天終結時想要匯總營業收入。對於這位店主來說，一種選擇是「按照隨機順序計算到手的現金和賬單」。勒貝格把這樣一位零售商稱為「缺乏系統觀點的」人，他依次累加收集起來的款項：1美元，10美分，25美分，另1美元，10美分，如此等等。這種方法猶如當他們從左至右越過區間[a, b]時提取遇到的函數值。對於黎曼積分，這個過程是由定義域中的值「驅動」的，而值域中的值被擱置一旁。

1 Henri Lebesgue, Measure and the Integral, Holden-Day, 1966, pp. 181-182。

勒貝格接著指出，如果不這樣做，店主在結賬時不考慮收到每筆款項的順序，而代之以按款項的面值分組，難道不是更為可取嗎？例如，可能共計收到10美分12筆，25美分30筆，1美元50筆，等等。這樣，計算一天的收入將變得很簡單：用每種幣值的數量（對應於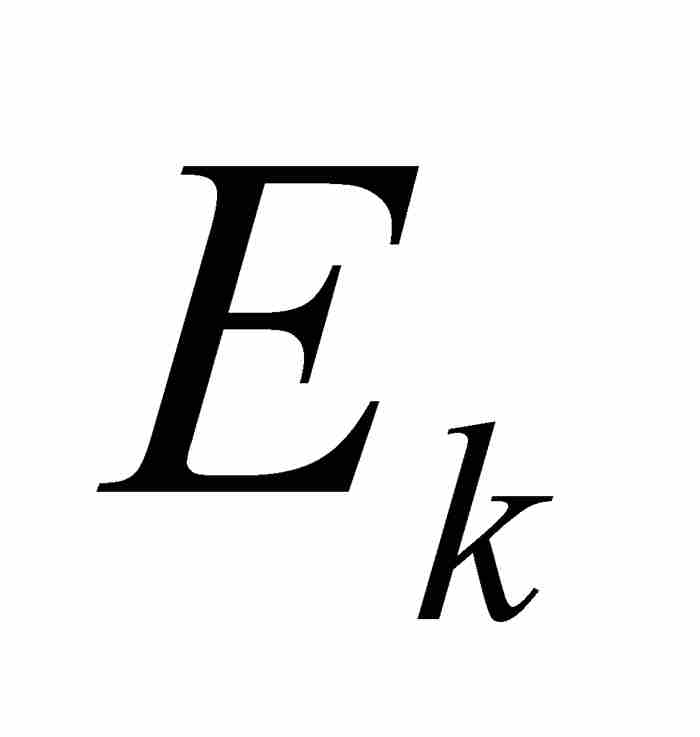的測度）乘以幣值（對應於函數值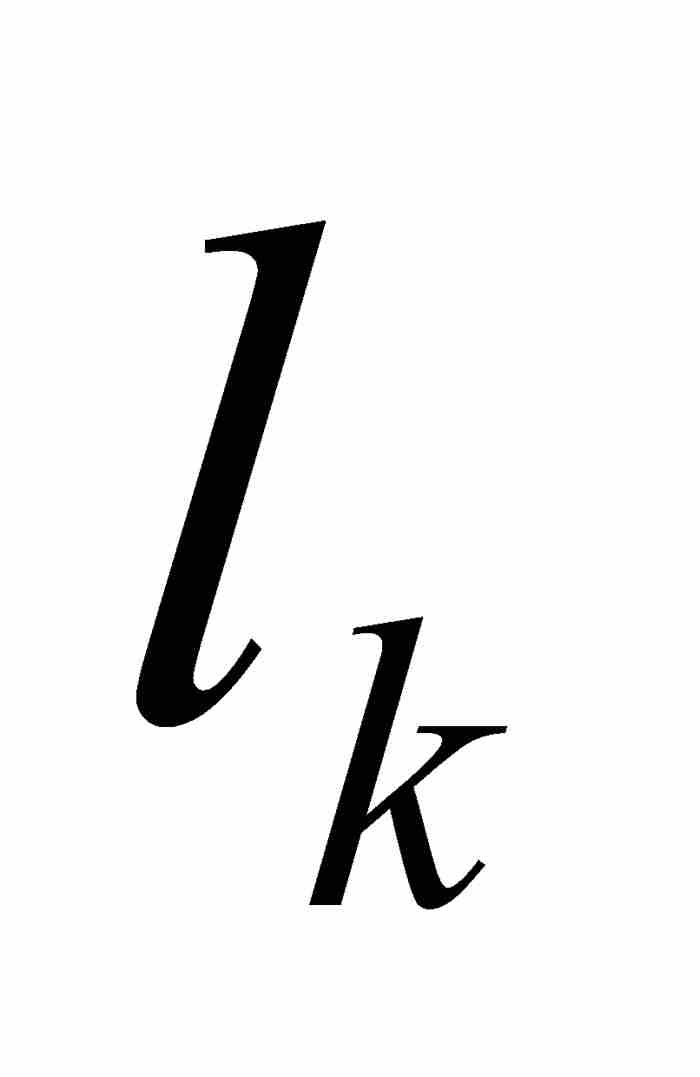），然後對結果求和。這種情況下，正如勒貝格積分的情形，其過程是由值域中的函數值驅動的，而劃分定義域的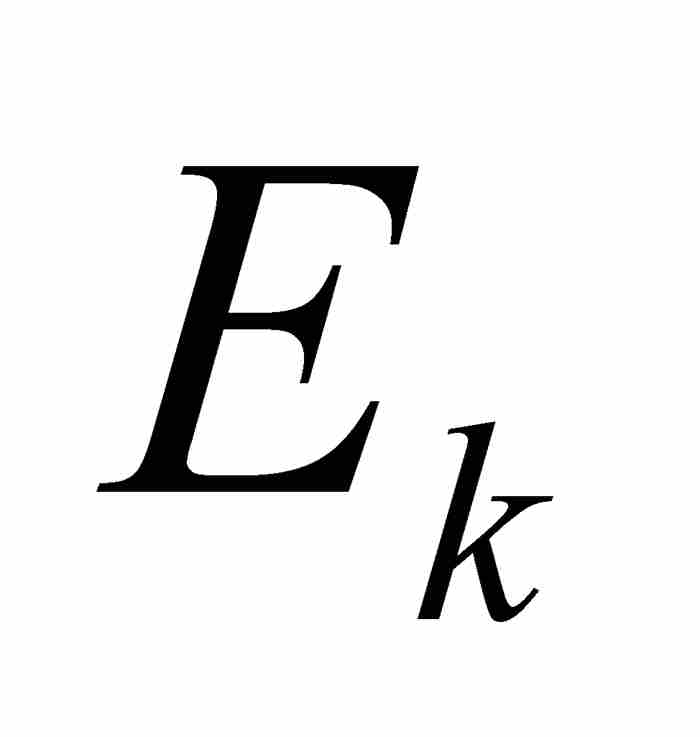被擱置一旁。

勒貝格承認，對於商業經營中涉及的有限的量，這兩種方法產生同樣的結果。「但是對於我們必需求數目無限的極微小的量之和而言，」他寫道，「這兩種方法之間存在著巨大差別。」為了強調這種差別，他指出：

我們的積分的構造定義，同黎曼積分的定義十分相似。不過，黎曼是把變量x改變的區間剖分成微小的子區間，而我們則是剖分函數f?(x)改變的區間。2
2 Henri Lebesgue, Lecons sur l'integration et la recherche des fonctions primitives, AMS Chelsea Publishing, 2000, p. 136。（這是我們在上面引用的勒貝格1904年的著作第2版的重印本，原書於1928年出版。）

為了說明自己並非漫無目標地追求定義，勒貝格證明了關於他的新積分的若干定理。我們將考察其中幾個定理，但是不予證明。

定理 1　地如果f(x)是區間[a, b]上的有界黎曼可積函數，那麼f是勒貝格可積的，並且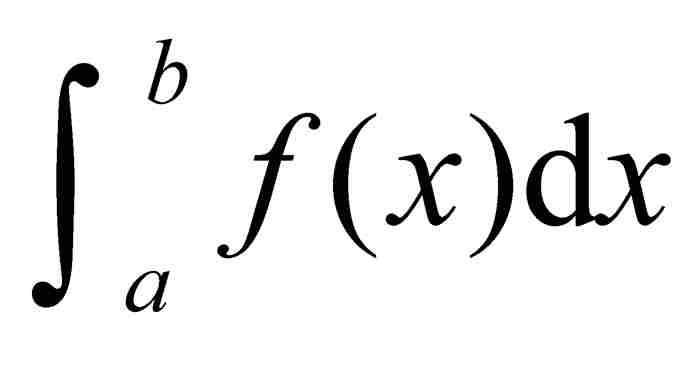在兩種情況下具有相同的積分值。

這個結果是令人欣慰的，因為它說明勒貝格積分保存了黎曼積分的精華。

定理 2　如果f(x)是區間[a, b]上的有界可測函數，那麼它的勒貝格積分存在。

我們從這個定理看出勒貝格思想的巨大力量，因為可測函數族包含的函數遠遠多於黎曼可積函數（即所有那些幾乎處處連續的函數）族。簡而言之，勒貝格可積的函數多於黎曼可積的函數。定理1和定理2表明，勒貝格名副其實地擴充了過去的理論。

例如，我們已經知道狄利克雷函數d(x)在區間[0, 1]上是有界的和可測的。因此，儘管事實上積分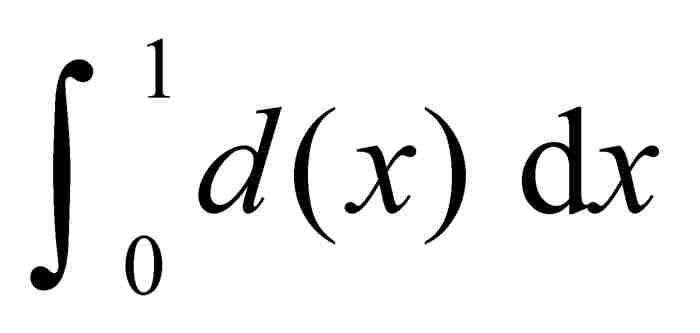在黎曼的理論下是沒有意義的，然而作為勒貝格積分卻是存在的。

更為可取之處在於，這個積分值是很容易計算的。我們從值域的任意劃分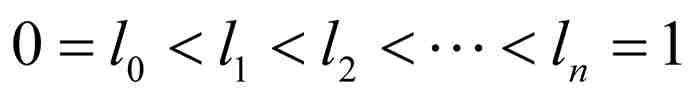著手。根據狄利克雷函數的性質，

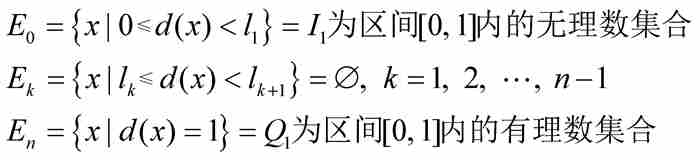
對於這個隨意的劃分，勒貝格和為

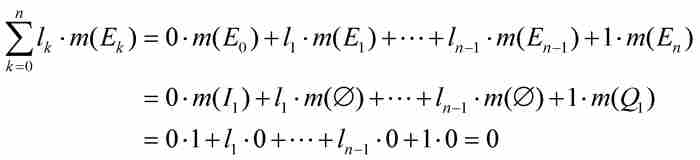
正是由於對於任意劃分這個勒貝格和為零，所以，所有這樣的極限也為零。也就是說，。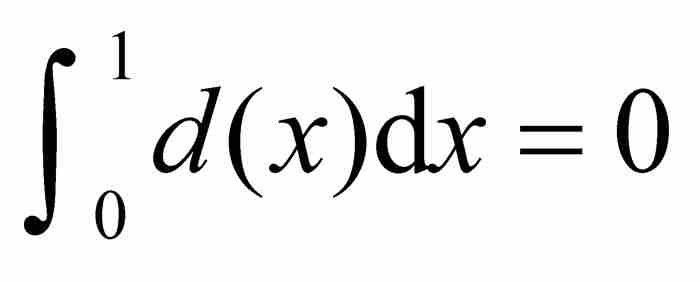

狄利克雷函數是處處不連續的這一事實，使它成為黎曼不可積的，但是這樣普遍的不連續性對於勒貝格積分是無關緊要的。這種結果無可爭辯地說明數學上取得的巨大進展。

定理 3　地如果f和g是區間[a, b]上的有界可測函數，並且幾乎處處有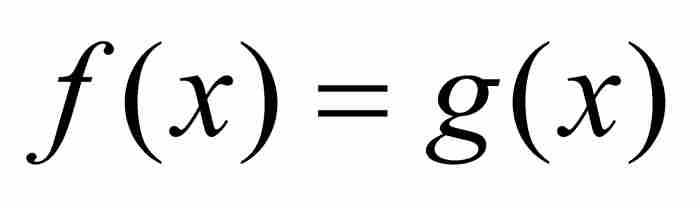，那麼。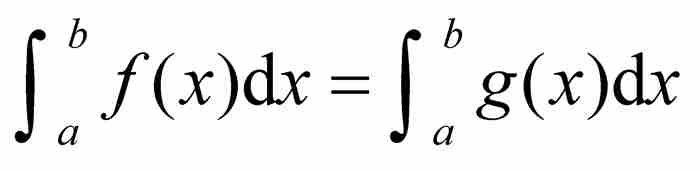

這個定理說明，改變一個可測函數在一個測度為零的集合上的值，對於它的勒貝格積分的值沒有影響。對於黎曼積分，如果改變函數在有限個點上的值，不會改變積分值，但是一旦胡亂修改無窮多點上的函數值，結果就無法預料了。相形之下，勒貝格積分具備足夠的抗變能力，我們可以在一個測度為零的無窮集合上改變函數值而不影響它的可積性和積分值。

為了考查這個定理的作用，我們重溫區間[0, 1]上的狄利克雷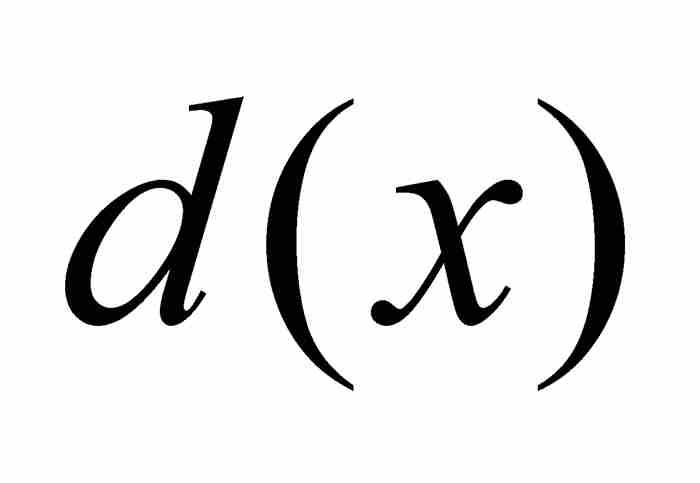函數和直尺函數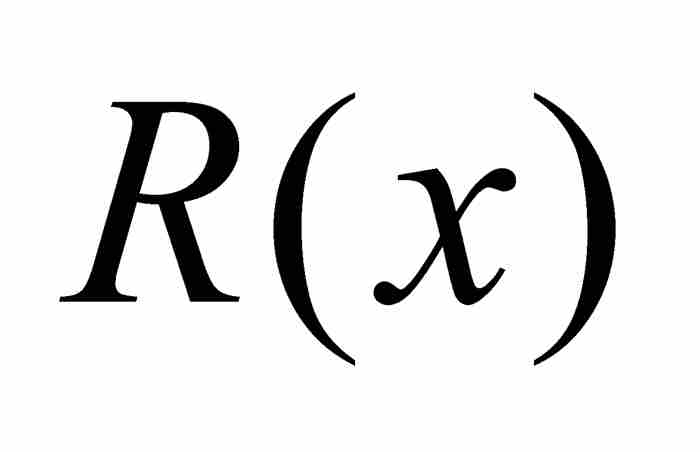，並且通過引進在[0, 1]上所有點都等於0的函數，組成一個三位一體的函數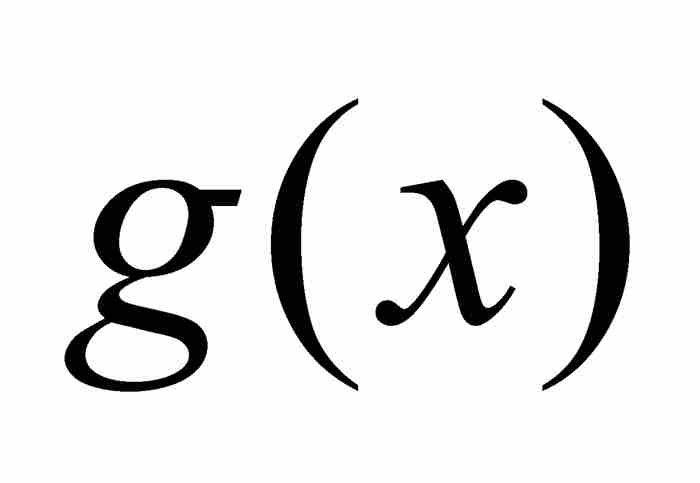。這三個函數d, R, g自然不是全等的，因為它們在單位區間的有理數點上具有不同的值。但是從測度理論的觀點看，這樣的差別是微不足道的，因為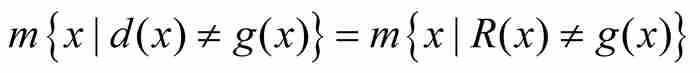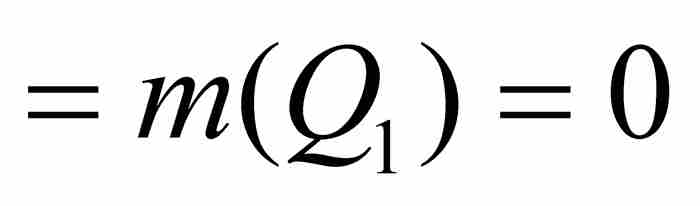。換句話說，狄利克雷函數和直尺函數幾乎處處等於零。由定理3推出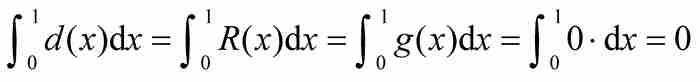，這正是我們過去見過的結果。

在勒貝格的論文中還有另外一個重要定理，那就是我們現在所說的有界收斂定理。3他在非常弱的條件下，證明了這個允許進行極限與積分的交換的定理。這是超越黎曼理論的一項重大進展。

3 Henri Lebesgue, Lecons sur l'integration et la recherche des fonctions primitives, Gauthier-Villars, 1904, p. 114。

定理4（勒貝格有界收斂定理）　如果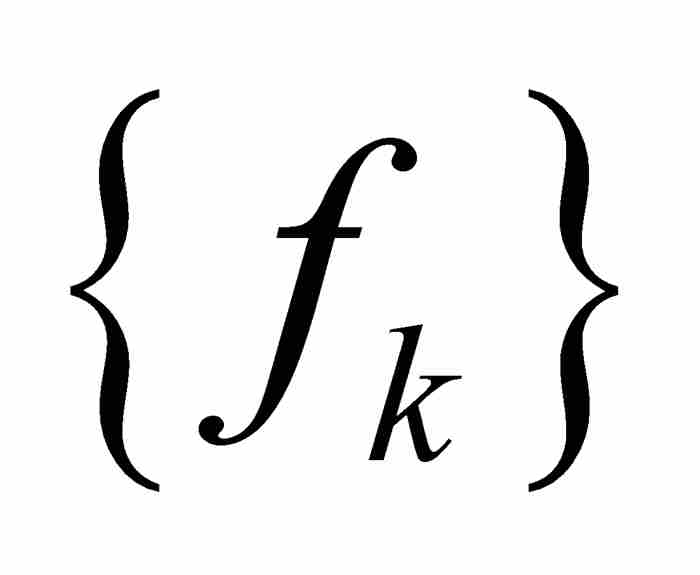是區間[a, b]上的可測函數序列，其中的函數以數M >0一致為界（即對於所有k≥1和[a, b]內的所有x有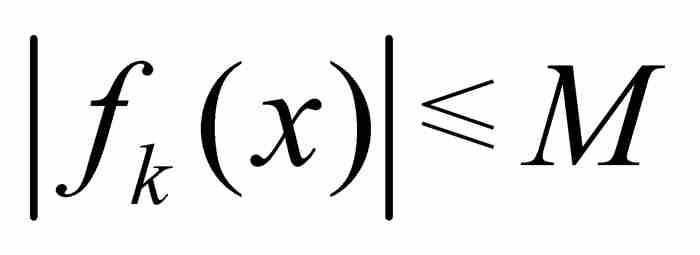），並且如果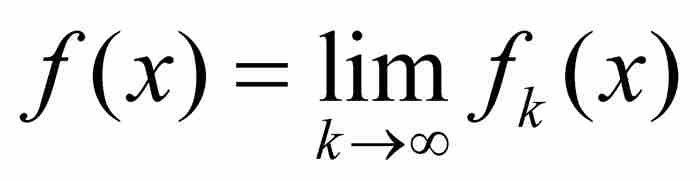是點態極限，那麼

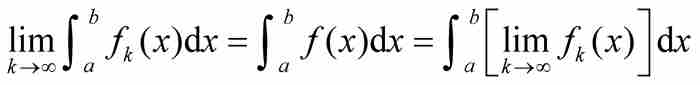
利用這個定理我們可以提出對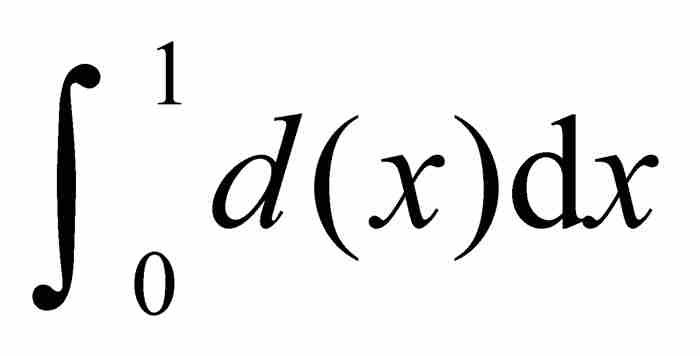的第三次處理。早先我們引進了區間[0, 1]上的一個函數序列，如在式（1）中所見，對於這個序列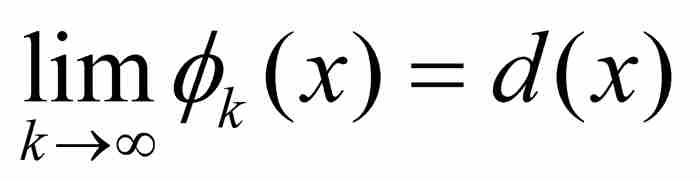，。顯然，對於所有x和全部k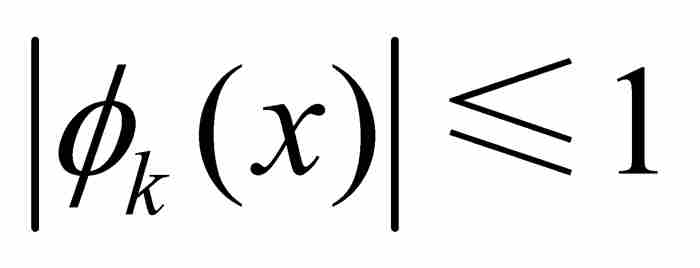，，所以這是一個一致有界的函數族，同時由於每個在除k個點之外為零，可知每個函數是可測的並且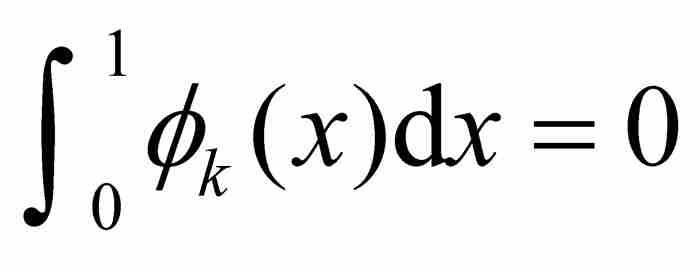。根據勒貝格有界收斂定理，我們再一次推出

勒貝格有界收斂定理的證明（1904）

時代鑄就一個人的最後成就。我們回憶一下，沃爾泰拉曾經發現一個病態函數，它具有有界而不可積的導數。在沃爾泰拉時代，「不可積的」自然是指「不是黎曼可積的」。

然而，採用勒貝格定義的替代積分，這個函數的病態特徵隨之消失。因為倘若F是具有有界導數F'的可微函數，那麼勒貝格積分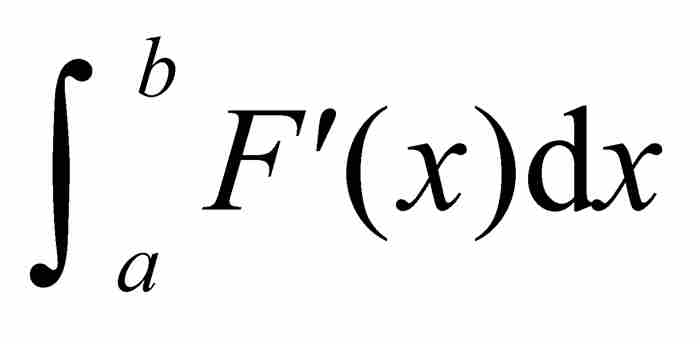必定存在，這正如我們在第13章所見，F'是屬於貝爾0類或貝爾1類的函數。這是使其成為勒貝格可積的充分條件。

有界收斂定理更值得稱道之處還在於，它使勒貝格得以證明下面的定理。4

4 Henri Lebesgue, Lecons sur l'integration et la recherche des fonctions primitives, Gauthier-Villars, 1904, p. 120。

定理 5　如果函數F在區間[a, b]上是可微的並且具有有界的導數F'，那麼。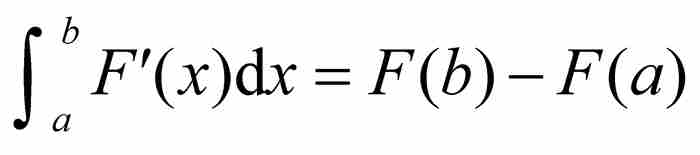

這是完全恢復原來的完美形態的微積分基本定理。對於勒貝格積分，為使基本定理成立，對導數無需附加限制條件，例如不必要求導數是連續的。因此，在一定的意義下，勒貝格把微積分中的這個處在中心地位的結果恢復成它在牛頓和萊布尼茨時代那種「自然的」形式。

在行將結束之際，我得承認，許許多多的技術細節在對勒貝格工作的這個簡短介紹中無法顧及。對他的思想的全面論述需要花費大量的時間和篇幅，那樣自然會使那些來自他的博士論文的思想越發令人驚歎！毫不奇怪，這篇學位論文出類拔萃，獨樹一幟。

我們引用勒貝格一則最終的評論作為結束語。在1904年那本重要的專題著作的序言中，勒貝格承認他的那些定理把我們從「優美的」函數之邦帶到一個更複雜的函數王國，而為了解決那些簡單陳述的具有歷史意義的問題，還需要在這片王國居住下來。他寫道：「這是為了解決已經提出的那些問題而不是出於對複雜事物的偏愛，我在書中引進一個積分定義，這個定義比黎曼積分的定義更具有普遍性，並且把黎曼積分作為一個特例。」 5

5 Henri Lebesgue, Lecons sur l'integration et la recherche des fonctions primitives, Gauthier-Villars, 1904, pp. v-vi。

為的是解決歷史留下的問題而不是為了使生活變得錯綜複雜化：這是亨利·勒貝格在他研究數學的旅程中所奉行的金科玉律。