附錄 概率論的基本原則

A.1 概率的概念

本書大部分內容所探討的都是對選擇的可能性、概率及其結果進行評估，所有此類未來的結果都會被看作是不確定的。此外，有實驗證據表明，即便我們相信未來是具有不確定性的，也會低估這種不確定性。因此，理性決策的關鍵在於要建設性地處理這種不確定性。非理性是沒有建設性的，至少由非理性得出的結論並不是對世界的真實反映。因此，概而言之，必須理性地對可能性和概率進行評估。

不確定性常常用概率（probability）或幾率（odds）這樣的形式來表達。一個事件發生的幾率等於這個事件的概率除以1與這個概率之差，比如，某事件發生的概率為2/3，1減去2/3等於1/3，因此2/3的概率就等於2比1的幾率，即（2/3）/（1/3）。當且僅當一組概率（或幾率）滿足四條廣義代數法則時，這組概率才是相容的，否則就是不相容的。這些極為簡單的法則稱為概率原則或概率論（probability theory）。附錄將會解讀每一條原則，我們會先在等概率結果的背景下（通常用拋硬幣和擲骰子來說明）探討與每條原則相關的概率，然後同時用代數和文字形式來呈現這些原則，最後則會在更廣義的背景中來討論。

因為我們是用概率的方式來評估和討論不確定性，這就意味著當且僅當我們為可能事件所賦的概率滿足這四條法則時，我們看待不確定性的方式才是理性的。只有滿足了這些法則，我們對於不確定性的看法才能說是相容或一致的（coherent），否則就是不相容的（incoherent）（字面上理解為「非理性」）。

不過在繼續之前，我們還要先澄清四點認識。第一，我們對概率的討論會限制在對未來事件的數字（或模糊數字）判斷。對決策者來說，過去的事件要麼是已經發生的（因而不是不確定的），要麼就是沒有發生，在這種情況下不能給它們賦予概率。當然，我們在提到過去事件的時候，常常會不太嚴謹地用到概率的說法，比如，我們也許會說到奧斯瓦爾德刺殺（或者單獨刺殺）肯尼迪的可能性有多大，一個被告「真的」犯了罪的可能性，或者某一枚假想中的硬幣在桌子上轉停後正面朝上的概率。然而，出於本書的考慮，這些關於過去事件概率的陳述，我們會將其解釋為在探尋真相時得到特定結論的概率，這當然就是一個具有可能性的未來事件。第二，有的時候我們會把概率解釋為「關於某看法的確定性程度」（degree of belief），或是在大量重複中的客觀頻率。不過，所有學習和研究概率論的人員都同意概率必須要滿足四條基本法則。（事實上，研究概率的抽像數學分支只將它們定義為遵循這些法則的數字，而不考慮附加到概率上的具體解釋和其他意義。）

第三，這個附錄也會考慮一些對概率的相關看法，包括對概率進行排列和歸類，這些看法同樣可能會出現滿足或違反概率原則的情況，因此也會反映出我們所做的判斷是否是相容的。舉例來說，當我們對某位世界頂尖網球運動員的比賽情況進行預測時，如果我們認為他在某場錦標賽上輸掉第一盤比賽並且最終贏得比賽的可能性要大於其單單輸掉第一盤的可能性（一個純粹的對於順序的看法），那麼這種看法就與概率論的原則相矛盾。類似的情況還有，我們會認為在已知某個症狀的情況下能夠確定罹患疾病的概率必定與已確定罹患某個疾病的情況下某個症狀出現的概率是相同的（沒有給定具體數字時的等價看法）。

第四，「非理性」這種說法隱含了一個前提，即所指的必須是包含兩個或以上概率的組合（除非違反最簡單的限制，將概率設為小於0或大於1的情況也是非理性的），因為我們無法在割裂的情況下評估某個概率判斷是不是理性的。舉例來說，如果有人認為有0.9的概率明天太陽不會升起，這種看法不一定是非理性的，然而，當你帶著這樣的看法，以及你明天有0.8的概率去上班且只有在太陽升起的情況下你才會去上班這樣的看法——同時具有這些看法，這才會是非理性的。[關於在概率評估（以及整體決策領域）中所出現的非理性有這樣一種解釋，即人們在看待一個問題的不同部分時，會在不同的思維狀態之間搖擺，在一個狀態下得到的結論不會與其他狀態下得到的結論進行比較——同樣也是基於這種考慮，經濟學家會假定偏好或偏好背後的效用是穩定的。我們將那些價值和預期經常搖擺不定的人判斷為「非理性的」，雖然從技術層面來看這種判斷可能不太正確，但要說他們是理性的或者是具有適應性的，顯然也不太合適。]

A.2 從神明到數字

概率論是如何開始的？概率論起源於對賭博的評估[我們推薦Leonard Mlodinow所著的《醉漢走路：機率如何左右你我的命運和機會》（The Drunkards』Walk: How Randomness Rules Our Lives， 2008），該書對概率論的歷史做了一個引人入勝的介紹]。

在Robert Graves所著的《羅馬帝國興亡史》（I, Claudius， 1943）一書中，卡力古拉[1]遇刺之前正在與克勞狄烏斯[2]玩骰子（一邊觀看血腥的遊戲，時不時地下令將輸掉遊戲的人[有時候也會是贏的人]處死）。他們所用的4顆骰子是由狗或羊的踝骨所做，稱為距骨（astragali），每顆骰子有4面，每一面有一個數字：1、3、4和6，所擲出的獲勝組合稱為維納斯列（Venus roll），需要4顆骰子擲出的數字各不相同。克勞狄烏斯一直在贏——而這樣的狀況讓他命在旦夕，因為輸掉的卡力古拉隨時會爆發病態的怒火。於是克勞狄烏斯戰戰兢兢地向卡力古拉獻上了一組打造得極為精美的新距骨骰子，據說這組骰子上附有神的力量，能夠擲出維納斯列。隨後卡力古拉又把他的錢贏了回來，他感到特別高興，因為他覺得維納斯神那天對他特別眷顧。他在得意忘形之際放鬆了警惕，最終被刺身亡。

（今天我們大多數人都會認為卡力古拉是迷信和愚蠢的，不過對這一事件人們也有一些其他的觀點。克勞狄烏斯將傳說附有神力的骰子獻給卡力古拉，騙他相信維納斯神會眷顧自己——而事實上卡力古拉之前的失敗說明維納斯神並不站在他那一邊。因此，克勞狄烏斯的欺騙行為也在一定程度上令他背上了行刺主謀的罪名，人們認為是他一手操縱這個事件幫助自己登上了王位。）

我們應該如何確定維納斯列的概率？以從左至右（可以從任意方向）的順序考慮距骨骰子的4個數字，並假定在這個例子中一顆骰子擲出4個數字的可能性相等。那麼「1」可以出現在4個位置中的任意一個，「3」可以出現在剩下3個位置中的任意一個，「4」在剩下2箇中的任意一個，「6」的位置也隨之確定。因此，一共有4 × 3 × 2 × 1 = 24種情況可以得到維納斯列，而所有可能擲出的序列則是44（即256）種，因為4個數字中任意一個都能出現在第1、第2、第3和第4個位置上。因此，我們得到結論，擲出維納斯列的概率為24/256，即大約0.094。

還有一種方法也可以得到相同的結論。依次考慮4個位置，在第1個位置出現任意數字都有可能得到維納斯列，給定第1個位置的數字，第2個位置的數字可以選擇剩下3個數字中的任意一個，其概率為3/4，如果前兩位數字不同，第3位的數字必須是剩下2個數字中的一個，其概率為2/4 = 1/2，最後，如果前三位數字各不相同，那麼最後一位是剩下那個數字的概率為1/4。將這些概率「連起來」就得到1 ×（3/4）×（2/4）×（1/4）= 6/64 = 24/256，即大約0.094。（因為並非所有結果的可能性都相同，因此實際概率更低，約為0.04。）

根據歷史學家Florence N.David（1962）的觀點，在古埃及、古希臘和古羅馬文明中，許多人都相信博弈的結果是由神明或超自然力量（「命運」）所主宰的（即便到了今天，這樣的觀念也依然會以一些內隱的形式存在於許多衝動的賭徒身上），並且，不同的賭博結果往往與不同的神明聯繫在一起。事實上，這些有關賭博的信念也正是中世紀羅馬天主教會將賭博定為不合法的原因之一。一神論的上帝不會去「擲骰子」——而賭博卻是多神論的催化劑。

當然，並非所有的古希臘人和古羅馬人都相信賭博的結果受到神明的影響。在《論責任》（De Devinatione）的第二卷中，西塞羅寫道：

沒有什麼事情比擲骰子更不可預測的了（現代翻譯），而每個玩骰子的人總會在某個時刻擲出一個維納斯列，有時會連續擲出兩個甚至三個維納斯列。那我們是不是真的就要幼稚到斷言這種情況的出現是因為維納斯神顯靈而非純粹的運氣使然？

西塞羅認為在使用隨機儀器的賭博遊戲中，「運氣」決定了人們的成功，他顯然也明白特定的某一次或某幾次擲骰子的運氣（幾率）與長期頻率之間存在一定的關聯。但是西塞羅後來被害了，這說明理性並不能確保成功，只是增加了成功的可能性。事實上，就像我們之前所指出的那樣，在其他人不選擇理性的時候選擇理性可能會導致社會排斥。

西塞羅並沒有預見到，現代概率論的一個重要發展就是通過計數的方法來確定幾率。只有當算術發展起來使得複雜計算變為可能時，才能開始採用計數的方法——雖然希臘人在幾何學和邏輯學上能力出眾，算術則一直到文藝復興時期才在西方世界發展起來。卡爾達諾（1501~1576）第一個系統性地提出了這種計數方法。下面我們來看看如何通過計數推導出概率論的基本原則：

拋1次硬幣會出現2個可能結果中的1個：正面（H）或反面（T）。

拋2次硬幣會出現4個可能結果中的1個：HH（兩個正面）、HT（先正後反）、TH或TT（見圖A.1和A.2）。

拋3次硬幣會出現8個可能結果中的1個：HHH、HHT、HTH、HTT、THH、THT、TTH或TTT。

依此類推。

結果（outcome）是概率論中的一個技術術語，指的是一個試驗（如多次拋硬幣）的一個特定結果。事件（event）是結果的集合，這個貫穿於本書的概念是概率論的關鍵——即便有的時候用「事件」二字來表達這個概念會有些生硬。在這裡，集合（collection）不一定是指包含多個結果，因此一個事件可以只包含單獨一個結果。當然，一個集合也可能包含所有結果，一個包含所有結果的事件是一個完備（well-defined）事件，用S表示。

圖A.1　拋2次硬幣的可能結果

圖A.2　拋2次硬幣的可能結果的「樹狀圖」

拋2次硬幣會得到其中一種可能的事件。舉例來說，

A.事件「兩個正面」只包含一個結果HH。（這與事件「沒有反面」等價。）

B.事件「有且只有一個正面」包含結果HT和TH。（這與事件「有且只有一個反面」等價。）

C.事件「至少有一個正面」包含結果HH、HT和TH。（這與事件「最多有一個反面」和事件「沒有兩個反面」等價。）

諸如此類。

實際上，共有15（= 24-1）個事件包含至少一個結果：

包含1個結果的事件：

HH

HT

TH

TT

包含2個結果的事件：

HH、HT

HH、TH

HH、TT

HT、TH

HT、TT

TH、TT

包含3個結果的事件：

HH、HT、TH

HH、HT、TT

HH、TH、TT

HT、TH、TT

包含所有4個結果的事件：

HH、HT、TH、TT

對這每個事件都可以進行一個語言描述。（請試一下。）

我們可以看到，拋2次硬幣之後，會得到4個可能結果，以及15個包含至少一個結果的可能事件。事實上，出於完整性的考慮，數學家會定義16個可能事件，換言之，他們也會考慮沒有包含任何結果的事件，這個事件稱為空事件（null event）（「沒有事情發生」），用符號表示。那麼空事件是否只是一個由人們思維中的強迫性概念所生發出來的（虛無）結果呢？並非如此。空事件的概念對概率論的發展與概念零（zero）對我們數字系統的發展起著同樣重要的作用。零的概念一直到公元900年才被引入西方的計算之中，在此之前，人們用羅馬符號來表示10（X）、20（XX）等等，但是加減計算的時候比用符號0麻煩得多——舉例來說，X+XXX = XL，而用0就可以表示為10+30 = 40，其中一部分是以0加0等於0所得到的。

下面我們來說如何為事件賦予概率。我們會首先考慮結果可能性相等的情況，然後再推廣到其他事件。考慮將一枚公平的硬幣拋2次的情況，這裡的「公平」（fair）是指滿足下面兩個條件：

1.每次拋硬幣得到正面或反面的可能性相等。

2.連續拋擲多次所出現的結果之間沒有關係。

「公平性」的含義同時涉及硬幣本身和拋硬幣的人：第一個條件說明硬幣本身沒有偏向性且拋硬幣的人沒有也無法控制結果；第二個條件說明硬幣「沒有記憶」，也再次說明拋硬幣的人沒有也無法進行控制。（許多「主觀主義」統計學家認為公平性存在於觀察者的信念之中，也就是說當觀察者認為硬幣和拋硬幣的人滿足這些條件時，這個過程就是「公平」的。）在這兩個條件之下，有4個可能性相等的結果：HH、HT、TH和TT。

當結果發生的可能性相等時，一個事件的概率就等於這個事件中的結果數量除以所有可能的結果數量。如果拋2次硬幣，所有可能的結果數量為4。

A.事件「兩個正面」只包含一個結果HH，因此其概率為1/4。

B.事件「有且只有一個正面」包含結果HT和TH，因此其概率為（1+1）/4 = 1/2。

C.事件「至少有一個正面」包含結果HH、HT和TH，因此其概率為（1+1+1）/4 = 3/4。

依此類推。

根據標準記號規則，事件由大寫字母表示，其概率用p表示。舉例來說，如果A表示事件「全為正面或全為反面」，這個事件包含結果HH和TT，因此，p（A）=（1+1）/4 = 1/2。

A.3 概率論的原則

我們已經知道，概率是0到1之間的數字，並且p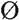（）= 0，因為空集中不包含任何結果。因此，下面這些原則適用於等概率結果的事件：

原則Ⅰ：0Gp（A）G1

原則Ⅱa：p（S）= 1

原則Ⅱb：p（）= 0

多個事件也可以聯合發生。事件A交B（A and B）稱為它們的交集（interse- ction），包含兩個事件共有的全部結果。舉例來說，事件「至少有一個正面」包含結果HH、HT和TH，而事件「至少有一個反面」包含結果HT、TH和TT，所以事件「至少有一個正面交至少有一個反面」包含結果HT和TH。（注意到這個事件與事件「有一個正面和一個反面」等價。）這樣的事件稱為復合事件（compound event），其概率稱為復合概率（compound probability）。（請注意，任意事件都可以看作是一個復合事件，每個事件首先都等價於其本身與全集S的交集。）

還有一種聯合方式涉及兩個事件中的任意結果。事件A並B（A or B）稱為它們的並集（union or conjunction），包含這兩個事件中的所有結果。（包含所有覆蓋到的結果，邏輯上即是指「兩個事件各自獨有的以及共有的結果」。）舉例來說，事件「至少有一個正面」 包含結果HH、HT和TH，而事件「至少有一個反面」包含結果HT、TH和TT，所以事件「至少有一個正面並至少有一個反面」包含結果HH、HT、TH和TT，即全集S（因為在任意一次「試驗」或拋擲中，肯定會出現至少一次正面或至少一次反面的情況）。

在這些例子中，兩個事件的交集或並集都有一部分重疊，不過正如前面提到過的，舉例來說，如果取一個事件與S的交集或與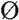的並集，這樣的情況就不一定發生。我們還可以取完全沒有重疊的兩個事件（即不包含共有結果的事件）的交集或並集，或者一個事件也可以是另一個事件的一個子集——即第一個事件包含的所有結果也全都出現在第二個事件中，或者兩個事件完全相同。事件是結果的組合，通過「交」或「並」將任意兩個事件聯繫起來就會定義一個新的結果組合，也就是一個新的事件。

如果兩個事件不包含共有結果，那麼它們是互斥的。舉例來說，事件「兩個反面」和事件「至少有一個正面」就是互斥的。

數學家和統計學家用空集來表達兩個事件互斥——即兩個事件沒有共同的結果。簡而言之，如果兩個事件A和B是互斥的，則它們的交集是空集（不含任何結果的集合）。因此只要

（A交B）=，

則A和B互斥，根據原則Ⅱ則得到

p（A交B）= 0。

再次考慮拋2次硬幣的情況。假設A是指事件「兩個反面」，B是事件「有且只有一個正面」，則這兩個事件是互斥的，前者包含結果TT而後者包含事件HT和TH。此外，A發生的概率為1/4而B的概率為2/4 = 1/2，（A並B）的概率為3/4，因為在（A並B）中共有3個結果，即TT、HT和TH。因此，p（A並B）= p（A）+ p（B）。

只要任意兩個事件A和B是互斥的，則（A並B）中的結果數量必定等於兩個事件中的結果數量之和。如果S中有n個可能性相等的結果，A中有m個而B中有m′個，如果A和B互斥，則

從這裡我們得到概率論的第三條普適原則：

原則Ⅲ：如果（A交B）=[等價於p（A交B）= 0]，

則p（A並B）= p（A）+ p（B）。

這個原則反過來是否成立呢？也就是說，如果p（A並B）= p（A）+ p（B），是否一定能得到（A交B）=？這個問題可以這樣來回答：如果A和B至少共有一個結果，那麼p（A並B）必定小於p（A）+ p（B），因此反過來也是成立的。

我們最後再引入兩個概念來完成對概率論的簡介。第一個是一個事件的補集（complement），具體來說，事件A的補集包含了全集S中所有不在A中的結果，A的補集通常用-A或來表示。舉例來說，考慮拋2次硬幣的情況：

如果事件A代表「兩個正面」（包含HH），則A的補集包含HT、TH和TT——即事件「至少有一個反面」。

如果事件A代表「有且只有一個正面」（包含HT和TH），則A的補集包含HH和TT——即事件「兩個正面或兩個反面」。

如果事件A代表「至少有一個正面」，則A代表事件「全為反面」。

等等。

關係Ⅰ：如果A是A的補集，則p（）+ p（A）= 1。

要推得這個關係，一方面因為A和互斥的，因此根據原則Ⅲ，p（A並）= p（A）+ p（），而根據定義，包括 S中所有不在A中的結果，因此（A並）等於S。所以，p（A）+ p（）= p（S），根據原則Ⅱa，結果等於1。

我們可以注意到原則Ⅱb，即p（）= 0，並沒有用來推導關係Ⅰ，關係Ⅰ完全由原則Ⅱa和Ⅲ推得。事實上，原則Ⅱb本身也可以看作是原則Ⅱa和Ⅲ通過關係Ⅰ推導出來的：因為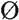是S的補集，所以p（）+ p（S）= 1，而由原則Ⅱa可得p（S）= 1，所以p（）= 0。（這個過程嚴格證明了空集的概率為空——零。）

最後需要指出，與原則Ⅲ不同，關係Ⅰ反過來是不成立的。如果兩個事件的概率總和為1，並不能說明它們互為補集。舉例來說，在拋2次硬幣且結果概率均等的情況下，事件「有且只有一個正面」和「有且只有一個反面」的概率都為1/2，相加等於1，但兩個事件的並集「有且只有一個正面並有且只有一個反面」的概率卻不等於1（1/2 +1/2），這兩個事件並不是互為補集。實際上，它們是相同的兩個集合，都包含結果HT和TH。

最後一個概念是條件概率（conditional probability），這可以很簡單地用一個公式來定義，但在給出這個定義之前，我們應先瞭解，條件概率的本質思想是事件A發生的概率能夠用另一種方法來評估，即根據另一個事件是否發生來分情況討論。舉例來說，我們考慮兩個極端的例子：如果事件A和B是互斥的，則A中的任意結果都不會在B中出現，那麼，當B發生的時候A發生的概率就為0；相反，如果B中的所有結果都出現在A中，那麼當B發生的時候A發生的概率就為1。

條件概率A當（given）B用符號p（AB）表示，可以用下面幾種不同的語言方式來表達：

1.在B發生的條件下A發生的概率

2.在B的條件下A發生的概率

3.當B發生時A發生的概率

4.如果B發生，則A發生的概率

如果不同結果的發生可能性都相等，則A當B就等於兩個事件中共有的結果數量（兩者的交集）除以B中的結果數量。實際上，「噹」B發生的時候，我們知道實際結果必定會從B之中選出，那麼此時A中的一個結果發生的概率就等於那些同屬於B和A的結果在B中的相對數量。事件B現在定義的是可能結果的數量，實際上也就代替了S。

用m′表示A交B（兩者的交集）中的結果數量，用m表示B中的結果數量，那麼，假設所有結果的可能性相等，則

p (AB) = m′/m。

現在將分式m′/m中的分子和分母分別除以n（n是全集S中的結果數量），得到

而因為p（A交B）= m′/n，而p（B）= m/n所以我們得到：

這個原則就是條件概率的正式定義。

現在我們來看看在拋2次硬幣的情況中條件概率的一些例子。事件「至少有一個正面」發生的條件下事件「兩個正面」的概率為1/3。（HH是事件「兩個正面」中唯一的結果，而事件「至少有一個正面」包含結果HH、HT和TH。）有的時候，人們會錯誤地認為這個概率是1/2而不是1/3。比如，有些人認為如果一個家庭中有兩個孩子，那麼在至少有一個女兒的情況下，有兩個女兒的概率為1/2。

而在第1次拋硬幣得到正面的條件下，事件「兩個正面」的概率就是1/2，此時共有的事件仍然是HH，但已經發生的事件只包含兩個結果，即HH和HT。仍然以有兩個孩子的家庭為例，在第一個是女兒的情況下，兩個都是女兒的概率為1/2，因為男孩（B）和女孩（G）出生的概率（大體）相等。對比來看，至少有一個女孩的情況則有三種：GG、GB、BG，這三種情況中只有一種情況（GG）下另一個也是女孩。因此，在至少有一個女孩的情況下有兩個女孩的概率為1/3，而不是1/2。

原則Ⅳ可以變換一下，寫成在p（B）基礎上「乘以」一個概率的形式，即

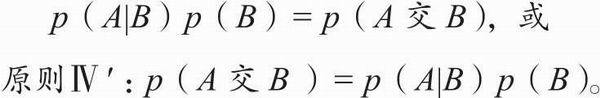
如果用原則Ⅳ′的形式來表達，條件概率的定義就包含了一個連鎖原則（chaining principle）來得到復合事件的概率。（請回憶一下維納斯列的例子。）舉例來說，拋2次硬幣都得到正面（事件「全為正面」）的概率就等於第1次得到正面的概率乘以當第1次得到正面時第2次得到正面的概率。讀者應該清楚這兩個概率都為1/2，因此得到這個復合事件的概率為1/4。在一副撲克牌中無放回隨機抽到2張黑桃的概率等於第1次抽出一個黑桃的概率（13/52，因為一副牌共有52張，其中有13張黑桃）乘以在第1次抽出黑桃的情況下再次抽到黑桃的概率（12/51，因為在餘下的51張牌中有12張黑桃）。從而得到這個復合事件的概率為（13/52）（12/51）= 3/51。我們也可以用兩張黑桃的組合數量（78）除以所有兩張牌的組合數量（1346），仍然能夠得到3/51。

連鎖從兩個方向都可以進行： p（A交B）等於p（AB）p（B），也等於p（BA）p（A）。有的時候從一個方向來考慮連鎖比另一個方向更容易一些——比如在時間上從前到後的自然順序。

最後，我們就可以定義事件之間的獨立性（independence）。獨立性的直覺定義是：如果p（AB）= p（A），則A與B互相獨立。接受這個定義後，我們在兩邊同乘以p（B），得到：

獨立性（定義）：p（A交B）= p（A）p（B）

（因為根據原則Ⅳ′可知p（AB）p（B）= p（A交B））。

此外，兩邊同除以p（A），我們也能推得p（BA）= p（B）。因此獨立性是對稱的。數學家們會採用p（A交B）= p（A）p（B）這個定義，因為當p（A）或p（B）等於0而不適宜進行乘除運算時這個概念仍然成立。

如今，概率論已被運用到除賭博遊戲之外更廣泛的情境之中。舉例來說，堤防和水壩是基於河流達到特定洪水位的概率估計而設計的，當然，工程師們並不會認為所有洪水位發生的可能性是相同的，而會參考過去達到某個洪水位的頻率來進行概率估計。我們也可能會說到在世界職業棒球大賽中芝加哥小熊隊打敗芝加哥白襪隊的概率，或者在公元3000年之前發生「原子戰爭」的概率。在這些情境中，我們沒有相關的頻率信息可用，而是要根據棒球、政治、技術的相關知識——或者可能是我們的悲觀程度來做出估計。如果結果既不是等可能的，也沒有頻率信息可以參考，概率往往與「純粹」的下注幾率有關。舉例來說，如果你認為小熊隊打敗白襪隊的概率為1/3，那你最多願意在白襪隊上下注2美元而在小熊隊上下注1美元，也就是說，你應該願意接受所有小於2︰1的賭博而拒絕所有高於2︰1的賭博，這是對你個人關於概率的看法的一種評估。實際上，有一群被稱為人格主義者（personalist）或主觀主義者（subjectivist）的概率哲學家認為，所有的概率本質上都是基於個人看法或賭博意願的。（舉例來說，在一個概率分析中，認為所有單個結果「發生的可能性都相等」這樣的基礎論點難道就不是一種主觀信念麼？）

實際上，幾個世紀以來，有關概率到底指的是事實還是個體對世界的看法，還是證據與看法之間（或不同看法之間）的邏輯關係，一直都存在很大的爭論。我們還不清楚這種爭論對概率推理究竟有多重要，不過我們清楚的是，雖然人們對概率這個概念的涵義會有不同的理解，但是對於特定概率他們會得到相同的結論。舉例來說，考慮這樣一個實驗，一個袋子中有兩顆骰子，其中一顆有4面綠色和2面紅色，另一顆有4面紅色和2面綠色，從中隨機摸出一顆，在不看到骰子的情況下直接擲骰子，結果得到紅色的概率是多少？所有參與實驗的被試認為是1/2，並且所有人都認為，這麼判斷的理由在於摸到兩顆骰子的概率都為1/2。

那麼為什麼人們會說摸到兩顆骰子的概率都為1/2呢？有些人說是因為我們沒有什麼理由能夠肯定自己摸到是其中的某一顆骰子而不是另一顆；有些人說1/2反映了自己的一種看法，即每顆骰子被摸出的可能性相等；有些人則說隨機的概念在邏輯上能夠推導出任意一顆骰子被摸出的概率為1/2；還有一些人則說摸到兩顆骰子的概率相等所基於的假設是一個可以通過重複實驗驗證其有效性的客觀事實；我們還可以說，無論是哪顆骰子，當它確實被摸出來時，其被摸到的「真實」概率為1，因為世界上並沒有什麼事是隨機發生的，只不過因為我們無法瞭解事件發生背後所涉及的所有因素及其交互作用，便只能選擇1/2。然而不管怎麼樣，所有這些都為這個實驗得出結論：摸出其中一顆骰子的概率為1/2。於是，擲出紅色面的概率可以由兩個部分組成，即4個紅色面的骰子摸出時擲出紅色面的概率，加上4個綠色面的骰子摸出時擲出紅色面的概率（根據原則Ⅲ）。第一個概率為（1/2）×（2/3），第二個概率為（1/2）×（1/3）（都根據原則Ⅳ′得到）。因此，擲出紅色面的概率為2/6+1/6 =1/2。結論得以證明。

那麼從普遍意義上來說，概率是什麼呢？第一，概率指的是對完備定義的事件所賦的數字。一個「完備定義的事件」（well-defined event）即是一個可以在未來毫不含糊地解釋為發生或不發生的事件。第二，概率必須滿足下面四個基本原則：

Ⅰ.0≤p（A）≤1

Ⅱ.p（S）= 1

Ⅲ.若交集（A交B）=，則p（A交B）= p（A）+ p（B）

Ⅳ.p（AB）= p（A交B）/ p（B）

許多哲學家還在試圖為概率找到更多的涵義，這樣的探討毫無疑問是極有意義的，不過目前我們也可以接受以這種結構化的方式來正式詮釋概率的涵義，即滿足這四個原則的數字。為配合本書的目的，我們加了一個額外條件——這裡考慮的是未來發生的事件。

我們注意到，除非這個數字落在了0到1的區間之外，單獨一個概率不會違反這些原則。因此，概率指的是描述一組事件之間關係的一組數字。當然，人們也許會維護那些違反規則的概率，堅持認為他們是在「概率」這個概念的常規涵義下進行討論的，但是理性或相容的概率必須滿足這些原則，這是數學家或統計學家所接受的唯一一種概率。

A.4 違反概率論原則的觀念

有許多常見的觀念是違反這些概率論原則的，舉例來說，考慮下面這些事件序列：

1.一位運動明星染上了毒癮，參加了一個治療課程，獲得了冠軍。

2.一位運動明星染上了毒癮，獲得了冠軍。

如果將其中一個事件序列呈現給人們，許多人會判斷第一種比第二種的可能性更高。但是根據概率原則，這是不可能的。要瞭解其中的原因，我們將這些序列中的事件進行分解：

A.這位運動員染上了毒癮。

B.這位運動員成了冠軍。

C.這位運動員參加了治療課程。

（不標注事件發生的順序）現在人們認為

p（A交B交C）〉p（A交B）。

但是這並不理性，或者說不符合這些原則，我們可以從兩個角度來證明：

證明1：根據連鎖原則（Ⅳ′），且因為交集（A交B）就是第二個事件，所以得到p（A交B交C）= p（CA交B）p（A交B）。

但因為根據原則Ⅰ，p（C[A交B]）G1，所以p（A交B交C）Gp（A交B）。

這是一個邏輯矛盾，證明最初的那個判斷是錯誤的。

證明2：（A交B）=（A交B交C）加上（A交B交），而（A交B交C）和（A交B交C）是互斥的，因此根據原則Ⅲ，

p（A交B）= p（A交B交C）+ p（A交B交）。

這就意味著p（A交B）必定大於等於右邊的第一項——又一個矛盾。其中的關鍵在於這位運動員可以通過治療課程之外的其他途徑最終獲得冠軍，他/她可能因為其他理由而戒掉了毒癮，可能具有極高的天賦或運氣，冠軍也可能是作弊得來等等。

對於一個不太可能發生的事件或事件聯合的可能性，人們會因為一些看似更合理事件的加入而增加其可能性，這種現象稱為情景效應（scenario effect），Amos Tversky和Daniel Kahneman（1983）對這類效應進行了深入的研究，發現這些加入的事件雖然在實際上限制了初始事件或事件聯合發生的可能性，但往往有助於構成一個「好聽的故事」。舉例來說，正如Paul Washburn（在與Dawes的私人交流中）所指出的那樣，當人類學家通過一些骨頭對某一個史前文化進行重構時，如果添加一些連自己都可能不太清楚的細節，這樣的重構往往看起來更為可信。我們也都知道，平平淡淡地把所知的事實告訴別人，不如將故事潤色一下來得有說服力（如在法庭最後陳述時）。認知心理學家已經發現了許多由情景效應所導致的非理性概率判斷（見第6章和第7章）。

下面是兩個有關概率的觀念，它們是錯誤的，但不是非理性的，然而把它們組合起來，就是非理性的。

賭徒謬誤：一個硬幣落下得到正面（反面）的次數越多，下一次拋硬幣時得到反面（正面）的可能性就越多。因此，HT比HH的可能性更高，HHT比HHH的可能性更高，諸如此類。[正如前面所說，這種觀念只有在硬幣有記憶（或者拋硬幣的人能夠控制的時候）才有可能是正確的。]

這種謬誤同樣會在其他情境中出現。考慮我們在章節7.3中所提到的 「致親愛的阿比」的例子：「我和丈夫剛剛有了我們的第8個孩子，又是一個女孩，我現在真的非常失望。……阿比，這個孩子應該是個男孩。」連續懷上8個女兒的概率（大約）為1/28 = 1/256，但是在其他7個女兒都已經生出來的情況下，再懷上一個女兒的概率為1/2。和硬幣一樣，精子沒有記憶，何況是過去那些它們完全不明真相的受孕情況。這個原則和2.6中所提到的balla遊戲的解答一樣。

未知分佈謬誤（將未知均等地分佈在人為定義的類別中，而不是特定的等可能結果上）：因為拋2次硬幣會得到0、1或2個正面，從這個偽原則會推出每個結果發生的可能性為1/3。

假設有的人同時相信賭徒謬誤和未知分佈謬誤，則根據賭徒謬誤，

p（HT）H p（HH）。

但是根據未知分佈謬誤，

p（HH）= 1/3。

因此，p（HT）H 1/3。同理可得，p（TH）H 1/3，所以兩者之和大於等於2/3，但根據未知分佈謬誤，兩者之和同時也應等於1/3（即「拋2次硬幣會得到0、1或2個正面」）。

有些觀念的組合是非理性的，然而人們還是會保留這些觀念。基於這些不相容的概率評估所做的選擇必定也是不相容的，甚至可能導致個人或社會傷害。而反過來的結論——滿足原則Ⅰ到Ⅳ的概率不會出現矛盾——也是正確的，不過相關的證明就不在本書中贅述了。

A.5 貝葉斯定理

假設我們有兩個袋子，裝著黑色和紅色籌碼。袋子A裝有70%的紅籌碼，而袋子B裝有40%的紅籌碼。有一個人會擲一顆骰子，如果得到1或2，則給我們袋子B，否則就給我們袋子A。我們不知道擲骰子的結果，因而也就不知道給我們的是哪個袋子，但我們可以從這個袋子中抽10次籌碼，每抽一次後都要把籌碼放回去再抽下一次。我們的任務是推測出所抽的是哪一個袋子。

假設我們抽出了6個黑籌碼和4個紅籌碼，這顯然更「像」袋子B而非袋子A，但是另一方面，我們知道根據擲骰子的結果，得到袋子A的可能性是袋子B的2倍。那麼，我們應該如何把抽出籌碼的證據和先前有關擲骰子的觀念結合起來呢？推而廣之，在獲得了一些相關的證據後，我們應如何理性地更新自己對於一個假設的看法（比如「現在是從袋子B中抽籌碼」這個假設）呢？

一種方法就是採用貝葉斯定理（Bayes』 theorem），這個定理是從概率論的第四個原則往後推了一步，通常認為是由Thomas Bayes教士提出。顯然，Bayes教士是在嘗試用理性的方式來證明上帝（我們想應該是基督教的上帝）的存在時發現了這個原則，但是他對自己的推導並不是很有信心，因此只將自己的發現與一個朋友交流過，Bayes在1761年去世之後，這位朋友才發表了他的發現。[對於想進一步瞭解貝葉斯分析的讀者，我們推薦Dennis V.Lindley所著的一本極佳的入門書籍《理解不確定性》（Understanding Uncertainty， 2006）。]

我們用d來代表已經收集的數據——6個黑籌碼和4個紅籌碼，用A和B代表兩個袋子。我們已經知道籌碼是從A、B這兩個袋子的其中一個之中抽得，因此很容易確定數據的條件概率。隨後如果我們知道一開始得到其中某個袋子的概率（我們已經知道了）以及得到這些數據的概率（可以通過計算得到），就能根據已有數據推出我們確實得到這個袋子的條件概率。具體來說，

p（A交d）= p（d交A）。

根據概率的第四原則，我們可推得

實際上，用5.10中的比例規則更為簡便，在這個情境中，

同理，

兩式相除，得到

通過這個除法，我們消去了麻煩的p（d），在最後一個等式中，我們得到的結果是p（Ad）除以p（Bd）的比例。知道了這個比例，以及這兩個概率之和等於1（我們是從兩個袋子之一中抽取籌碼，因此根據原則Ⅲ，概率之和為1），我們就很容易計算出這兩個概率。

在這個例子中，p（A）= 2/3，當我們從袋子A中抽取時，以某個特定順序抽得6個黑籌碼和4個紅籌碼的概率為0.36 × 0.74。同理，p（B）= 1/3，當我們從袋子B中抽取時，以同樣的順序得到這個樣本的概率為0.66 × 0.44。因此，p（Ad）除以p（Bd）= 0.0001167/0.0003981，即0.29。因此，6黑4紅10個籌碼是從袋子A中抽取的概率為0.22，從袋子B中抽取的概率為0.78。請注意，我們從這個假設的試驗中所得數據的信息價值要遠遠高於初始幾率所給出的信息——2︰1的幾率得到袋子A。

普遍說來，貝葉斯分析會將初始看法具體化，這裡的初始看法是指在我們獲得樣本之前所持有的看法，在這個例子中，擲骰子的過程會令我們形成初始看法。隨後我們根據貝葉斯定理將抽取樣本所得的證據與初始看法合起來，就能運用概率論的規則來更新初始看法。

A.6 對巧合的事後分析

在日常生活中充滿了巧合。道斯的大女兒出生的日子是他母親的忌日，而小女兒則和他的母親同一天生日。多麼驚人的巧合啊！一個對概率論幾乎不瞭解的分析者也許會得出結論，這兩個巧合的概率為（1/365）2，即0.0000075。不過顯而易見的是，這個巧合反過來的話同樣也是非常驚人的——這麼一來出現巧合的概率也許是0.000015才更合理。再者，兩個女兒當然也能同一天生日，並且和祖母的生日或忌日是同一天，這又是一個驚人的巧合，因此概率應該再翻一倍，得到0.00003。另外，大女兒有視覺藝術天賦，小女兒則是短篇小說作家——於是她們的生日還可以與相關領域中某位名人的生日相同。於是還有許許多多名人的生日，從George Washington、Abraham Lincoln、Grover Cleveland、John F.Kennedy，到Omar Khayam、Mahatma Gandhi、Bertrand Russel和傳道書的各位作者。關鍵問題在於我們可以不斷挖掘，哪怕通過這樣的回溯要找到一個特定的巧合（比如同一天生日）看起來也許是不太可能的，但是，也很有可能會出現許多巧合。

要理解這個原則，可以考慮一下死亡的概率。我們會做出一個簡化的假定，即每天死亡的概率是相等的。於是，假設一個人的預期壽命為70歲（25568天），那麼在其中某一天死亡的概率為0.00004，但是在特定的某一天死亡的概率為1.00。或者考慮另外一個例子，如果我們完全隨機地從1到10 000中選擇一個數字，任意特定數字被選中的概率為0.0001，而同樣對某個被選中的數字，概率為1.00。有趣的是，在概率論還在發展之中的十八世紀，一些哲學家把0.9999的概率等同於「幾近確定」（moral certainty）。在死亡的那個例子中，就意味著我們幾乎可以確定自己能安然度過每一天。（因此，不要買保險了？或者至少不要在任何特定的某一天去買？）

上面這兩段主要是為了解釋一個重要的原則：雖然一個特定事件發生的概率可能接近於0，但是什麼事情都不發生的概率則絕對為0。

那麼，我們怎麼來確定一個巧合究竟是不是超感官知覺的體現呢？或者舉一個具體的例子，在一個有關地鐵中的助人行為的研究中發現，高個比矮個更可能助人，這個發現能否說明身高和利他性之間存在相關呢？還有，從1900年到1968年，美國總統候選人中身高更有優勢的都贏得了選舉，這又是否意味著美國選民更喜歡高個子的人呢？

要回答這類問題並不容易，不過我們可以用一個簡化的例子來做個參考。再次考慮從1到10000中隨機選擇一個數字。如果一個自稱擁有預知能力的朋友事先說出你會選擇數字973，而你確實選擇了這個數，你就會感到非常震驚。相反，如果他/她先讓你選擇一個數字，在你說出973之後再向你解釋這個數字和他/她的預知能力之間有什麼特別的關聯，你就一點也不會覺得神奇。同樣是973這個數字，你既有可能感到敬畏，也可能完全不屑一顧，這取決於你的朋友是如何讓你瞭解這個數字的神奇之處的，具體而言就是你朋友所採取的決策過程以及你的決策過程。如果你的朋友事先說出數字，這樣你就只會把973這一個數字看作「成功」預知，你在選擇數字之前就能確認這個決定。然而，如果你的朋友是在你選完數字後才向你解釋這個數字的特別之處，你就很容易懷疑許多其他的數字也都能讓他/她說出某些「特別之處」。圖A.3就展示了這個原則。圖中呈現了拋6次硬幣所得到的一些正反面結果模式，這16種模式事後都能夠描述出一些特別之處（全為正面、全為反面、交替、2個一組交替、鏡像等等）。於是，如果人們拋6次硬幣，出現其中一種有趣模式的概率就不再是1/64，而是16/64。

圖A.3　隨機拋6次硬幣可得的16種明顯的模式

人們會做出這樣的事後判斷嗎？人們是否認為這樣的模式是突出（significant）的？這裡所說的「突出」不僅僅是指日常生活用語的涵義，也包括技術、統計上的涵義——顯著性。考慮道斯遇到的一位佔星家的話：

這難道不是冥冥中的天意嗎？這裡的5個人之中有3個獅子座和2個巨蟹座，而福特總統也是巨蟹座的，也就是說3個獅子座和3個巨蟹座。我打賭這樣的概率幾乎為0。這類事情你們能解釋嗎？

有一種方法可以將這類事件中明顯的特異之處進行誇張，稱為選擇性終點法（optional ending point maneuver），統計學家（及職業魔術師）Persi Diaconis（1978）詳細描述了這種方法。這個技術被許多心靈學家所使用，主要的技巧是始終不讓淳樸的觀察者確切瞭解事情的目標，直到達到目標為止。舉例來說，Diaconis曾詳細分析過心靈學者B.D.，他會讓一個觀眾說兩張牌，隨後請另外兩個觀眾「隨機」選擇兩個較小的數字。然後他會將兩疊洗過的牌放在桌子上，一張張地同時翻開兩疊牌。有的時候，他會在所選兩個數字中較大的那個出現時停止翻牌，如果在這之前第一個觀眾所說的兩張牌恰巧都出現過了，這當然就是一次「成功的表演」。他還有許多其他的選擇，比如要是兩張牌同時翻開，那顯然也是成功的，或者如果其中一張牌隨著那個大數一起翻開，這也還是成功的。如果沒有什麼「特別」的事情發生，那麼其中一疊牌會繼續翻下去，直到翻到較小的那個數字，到那個時候，所有類型的結果可能都出現過了。諸如此類不勝枚舉。這種選擇性終止詭計（optional stopping trick）就是事先不告訴別人你要如何操縱你的心靈力量，於是巧合的概率就會變得非常大。此外，如果你宣稱自己的力量來無影去無蹤，連你自己也無法解釋，或者說懷疑性的測試過程會對其產生干擾，這同樣有助於鞏固你的超能力形象，心靈學家Uri Geller就是這麼做的。於是，如果你多次嘗試後（甚至在過半的嘗試中）都沒有發現一些令人驚奇的巧合，觀眾也就願意表示理解。

「科學家們」是否會加入這樣的無稽之談呢？遺憾的是，答案是「會」。（有些分析師甚至推測，科學家們因為有能力去迎合一些並未得到證明的假設，甚至可能會特別容易相信超感官知覺或類感覺溝通。）美國心理學會近年的某一任會長在一次演說中發表了一個有關「轉矩與精神分裂易發性」的講話。在這個講話中，他呈現了一個令人極為震驚的數據，10年前他見過一群孩子並讓他們畫圈，在52名順時針畫圈的孩子中，有11名後來被診斷為精神分裂症，而在54名逆時針畫圈的孩子中，只有1名被診斷為精神分裂症。這個關係達到了「0.01的顯著性水平」。他將自己的發現與兩個事實聯繫了起來：其一是「地球是繞著南北軸逆時針旋轉的」，另一個則是「除了某些特例之外，這種『左旋』是生命細胞的特徵」。

這個量級的發現（尤其這個發現與地球和生命單位的基本屬性有關）顯然應該引起心理學界的注意，精神分裂症是美國最普遍的兩個心理健康問題之一（另一個是抑鬱），這個發現至少有助於我們進一步理解這個問題。在隨後的8年中，其他科學家對這篇文章的引用平均為每年3次左右，8年後這篇文章從排行榜上消失。為什麼引用量會那麼少呢？說不定這個研究者在長達50年的時間裡都不受大家重視，直到未來的某一天才被重新挖掘，從而成為精神分裂症現代理論的奠基人。然而，在他的演說中，我們能找到一個更有可能的解釋：「本研究的被試是155個孩子，這些孩子都是第一次在我的私人心理診所接受心理評估。」參加這類評估的孩子們往往會做許多測試，在每個測試中都會對大量的變量進行測量。然後，研究者在他的演說中只報告了這一個測試的研究結果，因而我們有理由推測，他也許已經將大量變量的測試結果與未來精神分裂症診斷的結果進行了簡單相關，而他演說中所報告的這個結果只是大約200個結果中的1個。（這裡需要強調的是，這種推測是基於筆者對臨床實驗的瞭解而得出的，並沒有實際看到這位研究者有許多測試。但是我們可以想像以下場景：一個孩子進入一位心理學家的辦公室，根據要求畫了個圈，然後就得以離開了。）

在這些極為不尋常的研究發現中，我們應該如何評價它們的重要性？最佳答案當然是要確定這個結果是否可以得到重複。有關此類「心靈力量」的重複嘗試基本都沒有得到什麼理想的結果。如果沒有預測、控制和重複的可能性，最佳方法就是事先精確地界定假設，界定可能的相關事件及其概念性樣本空間（conceptual sample space），隨後系統地收集數據（哪怕是奇聞軼事）來描述可能結果的全部空間（entire space）。Persi Diaconis和Fred Mosteller（1989）已制定了這樣一個策略，並將其闡述並應用於我們日常的一個實際經驗——我們會巧合性地「連鎖」遇到新學詞語。

只要我們的考察足夠仔細，就一定能發現一些東西。畢竟，完全沒有任何事情發生的概率確實等於0，並且正如Diaconis和Mosteller（1989）所說：「當大量的事件、人和兩者的互動隨時間累積，幾乎任何令人吃驚的事情都一定會發生」（p.853）。人們採用古典方法和貝葉斯方法來分析和檢驗統計顯著性，解決的都是事先提出的問題（questions asked beforehand）。在評估研究發現、從而做出理性決策的過程中，關鍵在於確定這些假設到底是事先提出的，還是僅僅是在事後，甚至是從聲稱發現了它們的人的想像之中提取出來。

參考文獻

David, F.N.(1962).Games, gods, and gambling: The origins and history of probability and statistical ideas fromthe earliest times to theNewtonian era.NewYork: Hafner.

Diaconis, P.(1978).Statistical problems in ESP research.Science, 201, 131–136.

Diaconis, P., & Mosteller, F.(1989).Methods for studying coincidences.Journal of the American Statistical Association, 84, 853–861.

Graves, R.(1943).I, Claudius.New York: Penguin.

Lindley, D.V.(2006).Understanding uncertainty.New York: Wiley-Interscience.

Mlodinow, L.(2008).The drunkard』s walk: How randomness rules our lives.New York: Pantheon.

Tversky, A., & Kahneman, D.(1983).Extensional versus intuitive reasoning: The conjunction fallacy in probability judgment.Psychological Bulletin, 90, 293–315.

[1] 卡力古拉，羅馬帝國第三任皇帝，父親是著名的凱撒大帝，卡力古拉被認為是羅馬帝國早期的典型暴君，後遇刺身亡。——譯者注

[2] 克勞狄烏斯，卡力古拉的叔父，原為羅馬的執政官，卡力古拉遇刺身亡後被近衛軍擁立為羅馬帝國第四任皇帝。——譯者注