「切」出一個體積最大的紙盒
數學是科學的語言，數學中用於表述大多數自然法則的是微積分。微積分是描述事物成長、變化與運動情況的數學分支。本章將討論如何確定函數變化率，如何利用多項式等簡單函數近似表示複雜函數等問題。此外，微積分是一個有效的優化工具，在我們希望某個數量最大化（例如利潤或容積）或最小化（例如成本或距離）時，可以幫助我們找到答案。
例如，假設你有一塊邊長為12英吋的正方形硬紙板（如下圖所示）。如果你從4個角上各切掉一個邊長為x的正方形，然後把剩餘部分做成一個紙盒，那麼這個紙盒的最大容積是多少？
x的值為多少時紙盒的體積最大？
首先，我們把紙盒的體積表示成x的函數。紙盒的底面積為(12 – 2x) (12 – 2x)，高為 x，因此它的體積應該是：
V = (12 – 2x)2 x
我們的任務是確定x取什麼值時紙盒的體積最大。x 的值不能太大，也不能太小。例如，如果 x = 0或 x = 6，紙盒的體積都是0。因此，x的值應該在0到6之間。
我們畫出x在0到6之間變化時函數 y = (12 – 2x)2 x的圖像。當x =1時，我們可以計算出體積 y = 100。當x = 2時，y = 128。當x = 3時，y = 108。看起來，x = 2有可能是最佳答案。不過，在1和3之間會不會有某個實數，讓盒子的體積最大呢？
函數y = (12 – 2x)2 x在最大值處有一條水平切線
在最大值的左側，函數呈上升趨勢，斜率為正值；在最大值的右側，函數呈下降趨勢，斜率為負值。因此，在最大值處，函數值既不再增大，也不再減小。用數學語言表述，就是最大值處有一條水平切線（斜率為0）。本章將討論如何利用微積分，在0到6之間找出有水平切線的那個點。
說到切線，我們將在本章看到種類繁多的切線。例如，我們剛才考慮的那個問題是找到切掉正方形硬紙板的四角的最佳方法。事實上，本章中有很多問題都是關於如何切掉邊角的。微積分這門課程的內容極其豐富，常用教材的篇幅往往超過1 000多頁。囿於篇幅，本書只關注其中最重要的內容，主要討論「微分學」（integral calculus，研究函數的增長與變化情況），而不涉及「積分學」（differential calculus，計算複雜對象的面積與體積）。
最容易分析的函數就是直線。我們在本書第2章瞭解到直線y = mx + b的斜率為m。也就是說，如果x增加1，y增加m。例如，直線y = 2x + 3的斜率為2，如果x的值增加1（比如從x = 10增加到 x = 11）時，y就會增加2（從23增加到25）。
在下圖中，我們畫出了若干條直線的圖像。其中，y = –x的斜率為–1，水平直線y = 5的斜率為0。
直線的圖像
取任意兩點，我們都可以畫出一條經過這兩點的直線。而且，無須知道這條直線的函數表達式，就可以確定它的斜率。如果直線經過點 (x1, y1) 和 (x2, y2) ，我們就可以根據「高度差與水平距離之比」這個公式計算出它的斜率：
m =
在直線 y = 2x + 3上任取兩點，例如(0, 3) 和 (4, 11)，那麼連接這兩點的直線斜率為 m = = (11 –3)/(4 – 0) = 8 / 4 = 2。計算結果與我們通過觀察方程式得到的結果一致。
接下來，我們考慮函數 y = x2 + 1（如下圖所示）。該函數圖像不是一條直線，它的斜率一直在變化。請大家計算點 (1, 2)處切線的斜率。
計算函數y = x2 + 1在點 (1, 2)處的切線斜率
令我們感到頭疼的是，我們需要知道兩個點的坐標才能計算切線的斜率，但現在我們只知道一個點 (1, 2)。因此，如上圖右側所示，我們先考慮經過曲線上兩點的直線（叫作「割線」），通過這條直線的斜率求出切線斜率的近似值。如果 x = 1.5，則 y =1.52 + 1 = 3.25。接下來，考慮連接點 (1, 2)與(1.5, 3.25) 的直線斜率。根據斜率公式，這條割線的斜率為：
m = =
=
= 2.5
利用割線斜率求出切線斜率的近似值
為了更好地求出切線斜率的近似值，我們讓第二個點向點 (1, 2) 靠近。例如，如果 x = 1.1，則 y = (1.1)2 + 1 = 2.21，於是新的割線斜率為 m = (2.21 –2)/(1.1–1) = 2.1。從下表可以看出，隨著第二個點不斷靠近點 (1, 2)，割線斜率趨近於2。
現在，令x = 1 + h ( h≠0 )，且與x = 1非常接近。那麼，y =( 1+h )2+1 = 2h + h2。於是，這條割線的斜率為：
隨著h越來越接近0，割線的斜率也會不斷地向2靠近。我們把這個現象表示成：
它的意思是，當h趨近於0時，2 + h 的極限值是2。憑直覺我們知道當h越來越接近0時，2 + h 就會不斷地向2靠近。由此我們發現，函數y = x2 + 1在點 (1, 2)處的切線斜率為2。
接下來，我們討論一般情況下的切線斜率。對於函數 y = f (x)，我們希望找出點 [x, f (x)]處切線的斜率。如下圖所示，經過點 [x, f (x)] 和其鄰近點 [x + h, f (x + h)] 的割線斜率為：
經過點 [x, f (x)] 和 [x + h, f (x + h)] 的割線斜率為
我們用符號 f '(x) 來表示點 [x, f (x)] 處的切線斜率，就有：
這個定義比較複雜，我舉幾個例子加以說明。對於直線 y = mx + b，有 f (x) = mx + b。要求出 f (x + h) 的值，我們可以用 x + h 替代x，即f (x + h) = m (x + h) + b。所以，割線的斜率為：
這表明斜率與x的值無關，也就是說f '( x ) = m，因為直線 y = mx + b 的斜率一定為m。
現在，我們利用這個定義求 y = x2 的「導數」（derivative）。對於這個函數，有：
=
=
=
= 2x + h
所以，當h趨近0時，我們可以得到 f ' (x) = 2x。
對於f (x) = x3：
=
=
=
= 3x2 + 3xh + h2
所以，當h趨近0時，我們可以得到 f '(x) = 3x2。
求已知函數 y = f (x) 的導函數 f ' (x) 的過程叫作「微分」（differentiation）。告訴大家一個好消息：一旦知道了一些簡單函數的導數，我們就可以輕鬆求出某些複雜函數的導數，而無須利用前文中介紹的基於極限的正式定義。下面這條定理十分有用。
定理：如果 u (x) = f (x) + g (x)，那麼 u' (x) = f ' (x) + g' (x)。換言之，和的導數等於導數的和。此外，如果c是任意實數，那麼 c f (x) 的導數是 c f ' (x)。
由於 y = x3 的導數是3x2，y = x2 的導數是2x，因此，根據上述定理，y = x3 + x2 的導數為3x2 + 2x。我們再舉一個例子，對上述定理的第二句話加以說明，函數 y = 10x3 的導數為30x2。
延伸閱讀
證明：令u (x) = f (x) + g (x)，那麼
=
=
+
當h趨近0時，對兩邊求極限就會得到：
u' (x) = f ' (x) + g' (x) □
請大家注意，在對這個方程式右邊求極限的時候，我們應用了「和的極限就是極限之和」這條定理。我們不準備給出關於這條定理的嚴謹的證明過程，但憑直覺就能知道，如果數字a趨近A，b趨近B，a + b就會趨近A + B。我們還注意到，「積的極限就是極限的積」，「商的極限就是極限的商」，這兩個說法同樣正確。但是，我們也將發現，導數的相關法則不像這樣簡單直接。例如，積的導數並不是導數的積。
就上述定理的第二句話而言，如果v (x) = c f (x)，那麼：
v' (x) =
=
= c
= c f ' (x)
證明完畢。 □
在求 f (x) = x4 的導數時，我們可以先列出函數展開式： f (x + h) = (x +h)4 = x4 + 4x3h + 6x2h2 + 4xh3 + h4。這個表達式的係數依次為1、4、6、4、1。看到這些數字，大家可能會覺得有些眼熟。原來，它們是我們在本書第4章裡見過的帕斯卡三角形第4行的數字。有了函數展開式之後，我們可以得到：
=
= 4x3 + h×(6x2+4xh+h2)
所以，當h趨近0時，就會得到 f '(x) = 4x3。看出其中的規律了嗎？ x、x2、x3和x4的導數分別是1、2x、3x2和4x3。即使指數繼續增加，這個規律仍然成立，因此我們可以得出下面這個非常有用的定理。另一個常用的導數符號是y'，從現在開始，我們就使用這個符號。
定理（冪函數求導公式）：對於nH0，
y = xn的導數為 y' = nxn–1
例如：
如果 y = x5，那麼 y' = 5x4
再例如：
如果 y = x10，那麼 y' = 10x9
常數函數，例如 y = 1，也可以根據這個規則求導。因為1= x0，因此，無論x的值是多少，y = x0 的導數都是0x–1 = 0。這個結果不難理解，因為直線 y = 1是一條水平線。結合冪函數求導公式和前文中給出的那條定理，我們可以求出任意多項式的導數。例如：
y = x10 + 3x5 – x3 – 7x + 2 520
y' = 10x9 + 15x4 – 3x2 – 7
即使n不是正整數，冪函數求導公式也成立。例如：
再例如：
但是，我們目前還無法給出證明過程。接下來，我們利用已學到的知識，解決一些有趣又實用的最優化問題。
最大值、最小值與臨界點
求導運算可以幫助我們確定函數值在何時達到最大或最小。例如，試求拋物線 y = x2 – 8x + 10的最低點的x值。
當 y' = 0時拋物線 y = x2 – 8x + 10處於最低點
拋物線最低點處的切線斜率必然等於0。由於 y' = 2x – 8，解方程式2x – 8 = 0可知，當 x = 4時函數的值最小（y = 16 – 32 + 10 = –6）。對於函數 y = f (x)，滿足 f ' (x) = 0的x值叫作函數f的「臨界點」（critical point）。例如，函數 y = x2 – 8x + 10只有一個臨界點： x = 4。
函數值在什麼時候最大呢？在上述問題中，由於y= x2 – 8x +10的值可以任意大，因此該函數沒有最大值。但是，如果x位於某個區間內，例如，0 G x G 6，那麼y值將在其中一個端點處達到最大。在這個例子中，我們發現當x = 0時，y = 10；當x = 6時，y = –2。因此，該函數值在端點 x = 0處達到最大。在一般情況下，我們有下面這條重要定理。
定理（最優化定理）：如果可導函數 y = f (x)在點x*處達到最大或最小值，那麼x*一定是函數f的臨界點或者一個端點。
我們再思考一下本章開頭提出的紙盒體積問題。要解決這個問題，就需要求出下列函數的最大值（x的值必須在0至6之間）：
y = (12 – 2x)2x = 4x3 – 48x2 + 144x
也就是說，我們希望找出y值最大時x的值。由於這個函數是一個多項式，因此我們可以求出它的導數：
y' = 12x2 – 96x + 144 = 12(x2 – 8x + 12) = 12(x – 2)(x – 6)
也就是說，該函數有兩個臨界點：x = 2和 x = 6。
在端點 x = 0和 x = 6處，紙盒的體積為0，也就是說，體積最小。在另外一個臨界點 x = 2，體積最大，即 y = 128立方英吋[1]。
一個關於奶牛的微積分問題
可以求導的函數越多，我們能夠解決的問題就越多。微積分中最重要的函數可能是指數函數 y = ex。這個函數之所以十分特殊，是因為它的導數與原函數相同。
定理：如果 y = ex，那麼 y' = ex。
延伸閱讀
f (x) = ex 為什麼滿足 f '(x) = ex 呢？現在，我們來探討其中的原因。我們注意到：
=
=
現在，請大家回想一下e的定義：
e =
( 1+
)n
從定義可以看出，隨著n不斷增大，(1 + 1 / n)n 將會趨近e。現在，令 h = 1 / n。當n非常大時，h = 1 / n就會趨近0。也就是說，當h 趨近0時：
e ≒ (1 + h)1/h
等式兩邊同時求h次冪，根據指數法則(ab )c = abc，可以得到：
eh ≒ 1 + h
也就是說：
≒ 1
因此，當h趨近0時，趨近1，趨近ex。證明完畢。 □
是否還有其他函數與它們的導函數相同呢？有，但所有符合條件的都是 y = cex （x為實數）這種形式的函數。（注意，c = 0時函數也符合條件，我們得到的是常數函數 y = 0。）
我們已經知道，函數相加時，和的導數就是導數的和。函數乘積的導數呢？千萬注意，乘積的導數並不是導數的乘積。不過，從下面的定理可以看出，乘積的導數也不難求。
定理（函數積求導法則）：如果 y = f (x) g (x)，那麼：
y' = f (x) g' (x) + f ' (x) g (x)
例如，在求 y = x3ex 的導數時，我們令 f (x) = x3，g (x) = ex，就有：
y' = f (x) g' (x) + f ' (x) g (x)
= x3ex + 3x2ex
注意，當f (x) = x3，g (x) = x5時，根據函數積求導法則，x3x5 = x8 的導數為：
y' = x3(5x4) + 3x2(x5)
= 5x7 + 3x7 = 8x7
這與冪函數求導公式一致。
延伸閱讀
證明（函數積求導法則）：令 u (x) = f (x) g (x)，就有：
=
接下來，我們採用一個巧妙的方法：在分子上先減去再加上 f (x + h) g (x)。這樣一來，在分子保持不變的情況下，我們把上式變成：
= f ( x + h ) [
] + [
] g ( x )
當h趨近0時，上式就會變成 f (x) g' (x) + f ' (x) g (x)。證明完畢。 □
函數積求導法則不僅可以用於計算，還可以幫助我們求出其他函數的導數。例如，我們在前文中證明當指數為正時，冪函數求導公式成立，現在我們可以證明當指數為分數和負數時，該公式也成立。
例如，冪函數求導公式表明：
我們現在用函數積求導法則來證明上述結果。假設
，那麼：
對等式兩邊進行求導運算，根據函數積求導法則，我們可以得到：
u (x) u' (x) + u' (x) u (x) = 1
也就是說，2u (x) u' (x) = 1，因此
，這同上述結果一致。
延伸閱讀
如果冪函數求導公式還可以用於指數為負數的情況，那麼根據該公式，y = x–n 應該有導數 y' = –nx–n–1 =
。為了證明這個結論，我們令 u (x) = x–n，其中 n H 1。根據定義，當x ≠ 0時，有：
u (x) xn = x–nxn = x0 = 1
運用函數積求導法則，對等於兩邊進行求導運算：
u(x)(nxn–1) + u'(x)xn = 0
兩邊同時除以xn，並將等式左邊的第一項移到等式右邊，就會得到：
u' (x) = –n
=
證明完畢。 □
因此，如果 y = 1 / x = x–1，那麼 y' = –1 / x2。
如果 y = 1 / x2 = x–2，那麼 y' = –2x–3 = –2 / x3。以此類推。
在本書第7章，我們希望找到一個正數x，使函數y = x + 1 / x的值最小。當時我們利用幾何知識，巧妙地證明了x = 1滿足條件。但是，有了微積分之後，我們就不再需要絞盡腦汁了。由 y' = 0可知1– 1/x2 = 0，所以滿足這個方程式的唯一正數就是 x = 1。
三角函數求導也非常簡單。注意，下面這條定理成立的條件是所有角必須用弧度來表示。
定理：如果 y = sin x，那麼 y' = cos x；如果 y = cos x，那麼y' = –sin x。換言之，正弦函數的導數是餘弦函數，餘弦函數的導數是正弦函數的相反數。
延伸閱讀
證明：要證明上述定理，需要使用下面這個「引理」（Lemma）。（引理的作用就是輔助證明定理）。
引理：
= 1且
= 0
這個引理的意思是，對於大小（弧度）接近於0的任意角h，其正弦函數接近於h，餘弦函數接近於1。例如，我們利用計算器可以算出sin0.012 3 = 0.012 299 6…；cos0.012 3 = 0.999 924 3…。暫且假設這條引理是正確的，我們就可以對正弦函數和餘弦函數求導了。利用第9章介紹的sin (A + B)恆等式，得出：
=
= sinx (
) + cosx(
)
根據引理，當h趨近0時，上式就會變成 (sinx) (0) + (cosx) (1) = cos x。同理，我們可以得到：
=
= cosx ( ) + sinx()
當h趨近0時，上式就會變成 (cosx) (0) – (sinx) (1) = –sinx。證明完畢。 □
延伸閱讀
利用下圖，可以證明=1。
該單位圓上有兩個點，分別為 R (1, 0)和P (cosh, sinh)，其中h是一個非常小的正數角。同時，在直角三角形OQR中：
tanh =
=
= QR
由此可知，直角三角形OPS的面積是
cosh sinh，直角三角形OQR的面積是ORQR =tanh =
。
現在，來看扇形OPR。單位圓的面積是 π12 =π，扇形OPS是單位圓的h/(2π)倍。因此，扇形OPR的面積為π(h/2π) = h/2。
由於扇形OPR包含三角形OPS，同時被包含在三角形OQR中，因此這三個圖形面積的關係滿足：
cosh sinh <
<
同時乘以
> 0，就會得到：
cosh <
<
如果正數a、b、c滿足 a < b < c，那麼1/c < 1/b < 1/a。因此：
cosh <
<
由於h趨近0，所以cosh 與1 / cosh 都趨近1。這與我們想要的結果一致。
也就是說， = 1。 □
延伸閱讀
有了上述結果，再通過代數運算（包括cos2h + sin2h = 1），就可以證明 = 0。
證明過程如下：
=·
=
=
= – ·
由於h趨近0，因此趨近1，且趨近
= 0。也就是說， = 0。□
知道正弦函數和餘弦函數的導數之後，就可以求出正切函數的導數了。
定理：對於 y = tan x，y' = 1 / cos2x = sec2x。
證明：令 u (x) = tan x = (sinx) / (cosx)，就有：
tanx·cosx = sinx
根據函數積求導法則，對等式兩邊同時求導：
tanx ·(–sinx) + tan'x·cosx = cosx
等式兩邊同時除以cosx，即可求出tan'x：
tan'x = 1 + tanx· tanx = 1 + tan2x =
= sec2x
上面倒數第二步是通過恆等式cos2x + sin2x = 1兩邊同時除以cos2x後實現的。
利用同樣方法可以證明函數商求導法則。
定理（函數商求導法則）：如果 u (x) = f (x) / g (x)，那麼：
u' (x) =
延伸閱讀
函數商求導法則證明過程如下：
因為 u (x) g (x)= f (x)，等式兩邊同時進行求導運算，根據函數積求導法則，可以得到：
u (x) g'(x) + u'(x) g (x) = f '(x)
等式兩邊同時乘以 g (x)：
g (x) u (x) g'(x) + u'(x) g (x) g (x) = g (x) f '(x)
把g (x) u (x) 替換成 f (x)，求出 u' (x) 的值，就會發現它與我們想要的結果一致。 □
我們已經知道如何對多項式、指數函數、三角函數等求導，還學會了函數和、積與商的求導方法，「鏈式法則」（chain rule）（本書將給出這條法則，但不提供證明過程）則會告訴我們如何對復合函數求導。例如，如果 f (x) = sinx，g (x) = x3，那麼：
f [g (x)] = sin [g (x)] = sin (x3)
請注意，該函數不同於函數g [f (x)] = g (sinx) = (sinx)3。
定理（鏈式法則）：如果 y = f [g (x)]，那麼 y' = f '[g (x)]g '(x)。
例如，如果 f (x) = sinx，g (x) = x3，那麼 f '(x) = cosx，g '(x) = 3x2。根據鏈式法則，如果 y = f [g (x)] = sin (x3)，那麼：
y' = f '[g (x)]g '(x) = cos [g (x)] g '(x) = 3x2cos (x3)
一般來說，根據鏈式法則，如果 y = sin [g (x)]，那麼 y' = g '(x) cos [g (x)]。同理，如果y = cos [g (x)]，那麼 y' = –g '(x) sin [g (x)]。
另一方面，對於函數 y = g [f (x)] = (sinx)3，由鏈式法則可知：
y' = g '[ f (x)] f '(x) = 3[ f (x)2 ] f '(x) = 3sin2x cos x
推而廣之，如果 y = [ g (x)]n，那麼y' = n[g (x)]n–1g '(x)。根據鏈式法則，如何對 y = ( x3 )5求導呢？
y' = 5(x3)4 (3x2) = 5x12 (3x2) = 15x14
這與冪函數求導公式得出的結果一致。
請大家計算
的導數。根據鏈式法則：
指數函數的求導運算同樣非常簡單。由於ex的導數就是它本身，因此，當 y = eg(x)時，根據鏈式法則：
y' = g '(x) eg(x)
例如，y = ex3 的導數為 y' = ( 3x2 ) ex3。
請大家注意，函數 y = ekx 的導函數為 y' = kekx = ky。指數函數之所以非常重要，這個屬性是原因之一。只要函數的增長速度與函數值的大小成比例關係，就會產生指數函數，指數函數在金融、生物領域中的出現頻率特別高。
對於任意x > 0，自然對數函數lnx 都具有以下特性：
elnx = x
下面，我們利用鏈式法則來求它的導數。令 u (x) = lnx，則eu(x) = x。對方程式兩邊求導，就會得到u'(x) eu(x) = 1。由於eu(x) = x，因此u'(x) = 1/x。換句話說，如果 y = lnx，那麼 y' = 1/x。根據鏈式法則，如果 y = ln [g (x)]，則 y' = 
。
我們把根據鏈式法則得出的這些結論匯總如下：
接下來，我們利用鏈式法則來解決「奶牛微積分」問題！一條小河由東向西流淌（x軸），奶牛克萊拉站在小河北邊1英里的地方，牛棚在克萊拉東邊3英里、北邊1英里的地方。克萊拉想去小河邊喝完水後回到牛棚。請問，要使克萊拉行走的路程最短，我們如何幫它找到飲水點的位置？
奶牛微積分：要使奶牛行走的路程最短，如何確定飲水點的位置？
我們還可以用第7章介紹的「映像法」來驗證這個答案。我們假設克萊拉喝完水之後，不是回到點(3, 2)處的牛棚，而是如下圖所示走到牛棚的映像點 B' (3, –2)處。
利用映像法，也可以解決這個問題
飲水點到點B'的距離與到點B的距離正好相等。從小河北邊的任意位置走到小河南邊都必須越過x軸，其中距離最短的路線是點 (0, 1)和點 (3, –2)的連線。這條直線的斜率是 –3/3 = –1，與x軸相交於 x = 1的位置。這種方法既不需要使用微積分，也不需要開平方！
泰勒級數與你的銀行存款
在上一章的結尾部分證明歐拉公式的過程中，我們使用了下面這些神秘的公式：
ex = 1 + x +
+
+ …
cosx = 1 – +
+ …
sinx = x – +
+ …
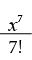我們先針對這些公式做一些小遊戲，再探究它們的由來。請大家對ex級數中的各項求導，並觀察得到的結果。例如，根據冪函數求導公式，x4 / 4! 的導數是 (4x3) / 4! = x3 / 3!，正好是它的前一項。換句話說，如果對ex級數求導，結果仍然是這個級數，這與我們瞭解到的ex的特性一致。
對 x – x3/ 3! + x5/ 5! – x7/7! + …這個級數逐項求導，就會得到1–x2 /2! + x4/4! –x6/6! + …，與正弦函數的導數是餘弦函數這個結論一致。同樣，對餘弦級數求導，就會得到正弦級數的相反數。此外，請大家注意，我們從餘弦級數可以得出cos0 = 1，而且由於所有的指數都是偶數，因此cos(–x)的值與cosx相等，這與我們瞭解到的餘弦函數的特性一致。[例如，(–x)4/4! = x4/4!。]正弦級數的情況與之相似，我們發現sin0 = 0，同時，由於所有指數都是奇數，因此sin(–x) = –sinx。
現在，我們來研究這些公式是如何產生的。本章已經介紹了大多數常用函數的求導方法，但有時候我們需要對函數進行多次求導，計算該函數的二階、三階甚至多階導數，記作f ''(x)、f ''' (x)等。二階導數f ''(x)表示點[x, f (x)]處函數斜率的變化率（亦稱函數的凹凸性）。三階導數表示二階導數斜率的變化率，以此類推。
上面這些神秘的公式以英國數學家布魯克·泰勒（Brook Taylor，1685—1731）的名字命名，叫作「泰勒級數」。如果函數 f (x) 有導數f '(x)、 f ''(x)、 f '''(x)等，那麼在x取任意「十分接近」0的值時，都有：
f (x) = f (0) + f '(0)x + f ''(0)+ f '''(0)+ f ''''(0)+ …
「十分接近」是什麼意思？對於某些函數而言，例如ex、sinx和cos x，x的所有值都十分接近0。但我們以後會發現，對於某些函數而言，x的值必須非常小，泰勒級數才會十分接近函數值。
我們來看冪函數 f (x)= ex的泰勒級數。由於ex 就是它自身的一階（二階、三階……）導數，因此：
f (0) = f '(0)= f ''(0) = f '''(0) = … = e0 = 1
也就是說，ex的泰勒級數是1 + x + x2/2! + x3/3! + x4/4! + …，這與前面給出的結果一致。當x比較小時，我們只需計算為數不多的幾項，就可以得出與確切答案非常接近的結果了。
我們用泰勒級數來計算存款的復利。在上一章，如果我們在銀行裡存1 000美元，年利率為5%，按連續復利的方式結算利息，那麼到年底時，銀行賬戶的金額就會變成1 000e0.05 = 1 051.27美元。利用泰勒多項式得到的二階近似值是：
1 000 [1 + 0.05 + (0.05)2/2!] = 1 051.25美元
三階近似值是1 051.27美元。
下圖是函數 y = ex以及它的前三階泰勒多項式的圖像，以展現泰勒級數逼近函數值的效果。
泰勒級數逼近y=ex的函數值
隨著我們增加泰勒多項式的階數，近似值會越來越接近函數值，在x取接近於0的值時，近似效果最好。泰勒多項式為什麼有這樣的作用呢？一階逼近（亦稱線性逼近）的意思是，對於接近0的任意x，都有：
f (x) ≒ f (0) + f '(0)x
這是一條經過點 [0, f (0)]的直線，斜率為 f '(0)。同理，我們可以證明，n階泰勒多項式在點[0, f (0)]處的一階導數、二階導數、三階導數直至n階導數都與原函數 f (x)相同。
延伸閱讀
我們還可以通過x接近除0以外的其他數字，來定義泰勒多項式和泰勒級數。具體來說，函數 f (x) 在基點 a 處的泰勒級數為：
它與x = 0時的情況一樣，對於十分接近a的x，無論x是實數還是複數，泰勒級數都等於 f (x)。
接下來，我們來看函數 f (x) = sinx的泰勒級數。再次提醒大家，f '(x) = cosx，f ''(x) = –sinx，f '''(x) = –cosx，f ''''(x) = sinx = f (x)。在x取0時，f (x)的n階導數會從 f (0)開始出現循環現象：0，1，0，–1，0，1，0，–1…。因此，x的所有偶數次冪都不會出現在泰勒級數中。也就是說，對於取任意值的x（單位為弧度），都有：
sinx = x – + – + …
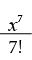同理，當 f (x) = cosx時，都有：
cosx = 1 – + – + …
最後，我再舉一例。在這個例子中，當x取某些值而不是所有值時，泰勒級數等於函數本身。我們來看函數 f (x) =
= (1 – x)–1，f (0) = 1。根據鏈式法則，我們可以算出該函數的前幾階導數：
f '(x) = (–1) (1 – x)–2(–1) = (1 – x)–2
f ''(x) = (–2)(1 – x)–3(–1) = 2(1 – x)–3
f '''(x) = (–6)(1 – x)–4(–1) = 3!(1 – x)–4
f ''''(x) = (–4!)(1 – x)–5(–1) = 4!(1 – x)–5
按照這個規律（或者使用歸納性證明法），就會發現 (1 – x)–1 的n階導數為 n! (1 – x)–(n+1)。當x = 0時，該n階導數就是 n!。也就是說，根據泰勒級數，我們可以得出：
= 1 + x + x2 + x3 + x4 + …
但是，這個等式只在x取–1到1之間的值時才成立。例如，如果x大於1，右邊各項的值會越來越大，它的和無法確定。
我們將在下一章繼續討論泰勒級數。大家可能會想，把無窮多個數字加在一起，到底有什麼意義呢？如何能求出它們的和呢？你有這樣的想法很正常。在研究無窮大的本質時，我會嘗試回答這個問題。與此同時，你還將接觸到大量你意想不到、讓你困惑、無法憑直覺理解但又充滿美感的內容。
[1] 1立方英吋≒16.387立方厘米。——編者注